Pyramid with a Quadrilateral Base.
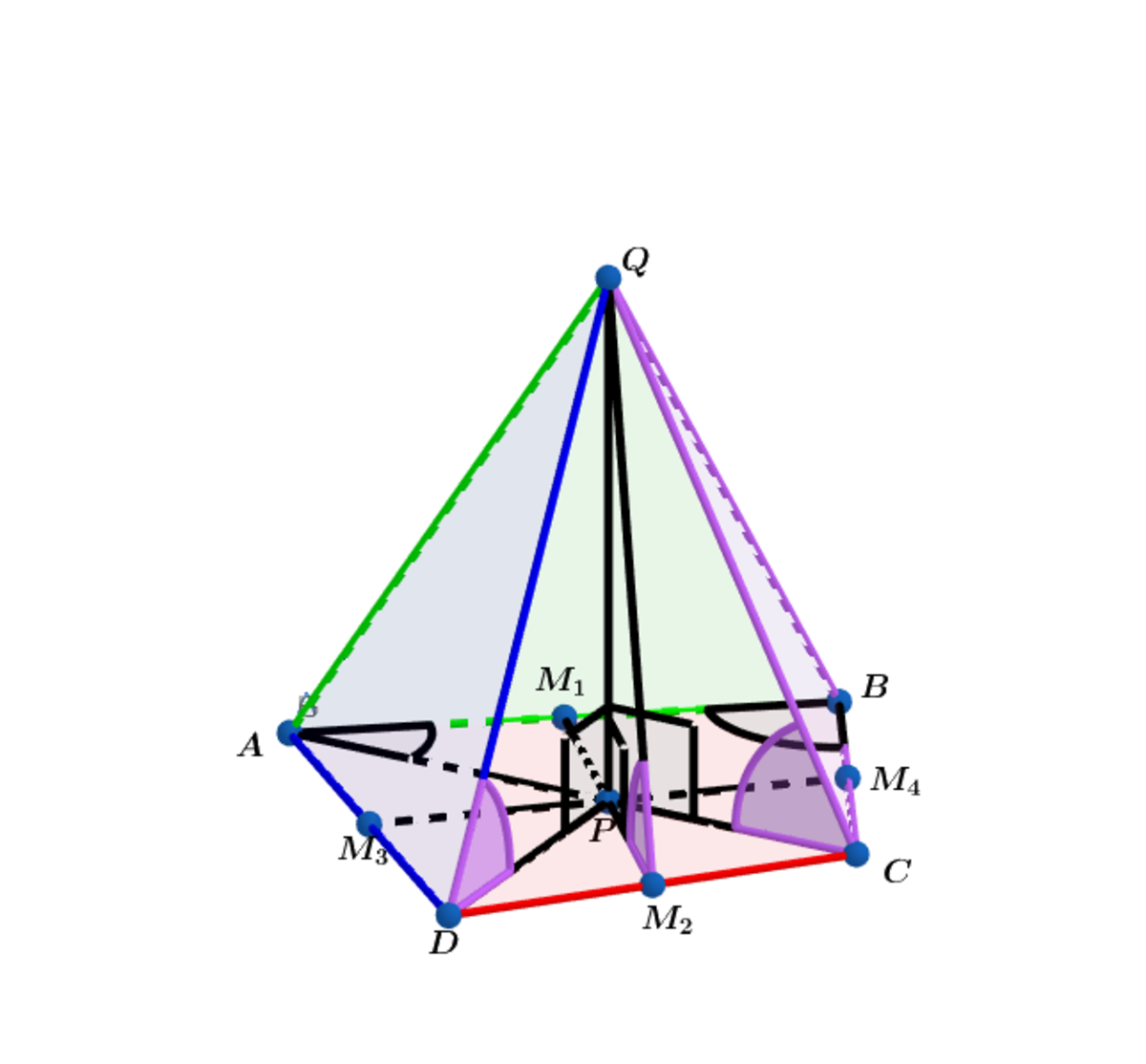
In quadrilateral , and are midpoints of and respectively, and is the centroid of quadrilateral obtained by finding the intersection of the bimedians.
In , is twice , and .
Let the height of the pyramid be .
(1): Find the (in degrees) that minimizes the triangular face .
(2) Using the values of and obtained in (1) , find the and the (in degrees).
Express the result as to seven decimal places.
The answer is 148.4848215.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Using the law of sines ⟹ sin ( β ) sin ( 2 β ) = m − 2 m ⟹ cos ( β ) = 2 ( m − 2 ) m
Using the law of cosines with included ∠ B A C ⟹ m 2 − 4 m + 4 = m 2 − 2 m + 1 + m 2 − m − 2 m 2 ( m − 1 ) ⟹ m 2 − 7 m + 6 = 0 ⟹ ( m − 6 ) ( m − 1 ) = 0 m = 1 ⟹ m = 6 ⟹ A C = 6 a , A B = 5 a and B C = 4 a
cos ( β ) = 4 3 ⟹ B D = 4 5 a 7 a and A D = 4 1 5 a
Using the above quadrilateral with the given coordinates:
m M 1 M 2 = − 1 2 5 7 ⟹ y = − 1 2 5 7 x + 3 2 4 5 7 a
and,
m M 3 M 4 = 1 2 5 7 ⟹ y = 1 2 5 7 x − 3 2 4 5 7 a
Solving the two equations above we obtain: x = 8 2 7 a and y = 0 ⟹ P ( 8 2 7 a , 0 ) which is a midpoint of each congruent bimedian.
For triangular face Q D C :
P M 2 = 8 3 1 9 a and h = P Q ⟹ Q M 2 = 8 6 4 h 2 + 3 1 9 a 2 and D C = 4 a ⟹ A = A Q D C = 2 1 ( D C ) ( Q M 2 ) = 4 a 6 4 h 2 + 3 1 9 a 2
A △ A B C = A △ A D C = 4 1 5 7 a 2 ⟹ A A B C D = 2 1 5 7 a 2 ⟹ the volume of the given pyramid is V = 2 5 7 a 2 a 2 h = k ⟹ h = 5 7 a 2 2 k ⟹ A ( a ) = 2 0 7 a 2 2 5 6 k 2 + 5 5 8 2 5 a 6 ⟹
d a d A = 1 0 7 a 2 2 5 6 k 2 + 5 5 8 2 5 a 6 5 5 8 2 5 a 6 − 1 2 8 k 2 = 0
⟹ a = ( 5 2 2 3 3 8 2 k ) 3 1 ⟹ h = 5 7 2 k ( 8 2 k 5 2 2 3 3 ) 3 2
Let θ = m ∠ Q M 2 P ⟹ tan ( θ ) = 3 1 9 a 8 h
a h = 8 2 3 1 9 ⟹ tan ( θ ) = 2 ⟹ θ ≈ 5 4 . 7 3 5 6 1 0 3 ∘
P D = 8 7 0 9
Let λ = m ∠ Q D P ⟹ tan ( λ ) = 7 0 9 8 a h = 7 0 9 6 3 8 ⟹ λ ≈ 4 3 . 4 8 9 2 7 7 5 ∘
P C = 8 2 1
ω = m ∠ Q P C ⟹ tan ( ω ) = 2 1 8 a h = 2 1 6 3 8 ⟹ ω ≈ 5 0 . 2 5 9 9 3 3 7 ∘
⟹ θ + λ + ω = 1 4 8 . 4 8 4 8 2 1 5 .