Pyramid with Rectangular Base 2.
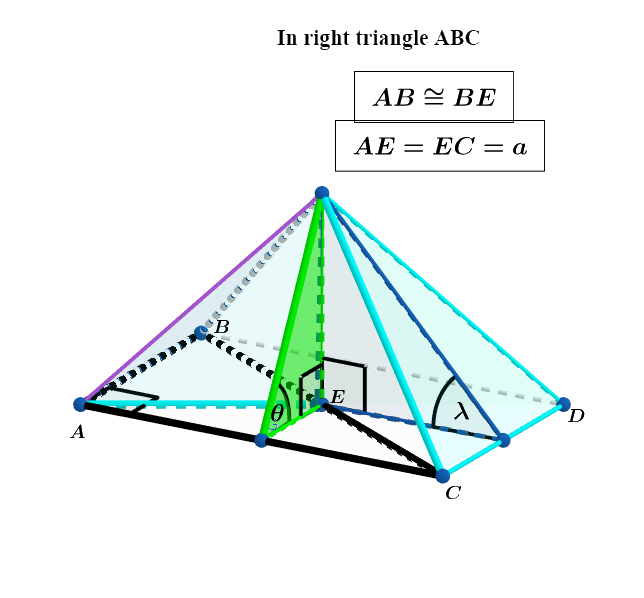
In the rectangular pyramid above, find the angle in degrees that minimizes the lateral surface area of the rectangular pyramid when the volume is held constant, and find the angle in degrees.
Express the answer as to six decimal places.
The answer is 1.312226.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
△ A E C is an isosceles triangle ⟹ E M is the perpendicular bisector of base A C ⟹ △ M E C is a right triangle and A M = M C .
Since ∠ A C B is a common angle to both right triangle A B C and M E C ⟹ △ A B C ∼ △ M E C ⟹ m 2 m = a x + a ⟹ x = a and the pythagorean theorem in △ A B C ⟹ y = 2 m = 3 a .
The lateral surface area S = 2 1 ( 3 a 4 h 2 + a 2 + a 4 h 2 + 3 a 2 ) and the volume V = 2 3 1 a 2 h = k ⟹ h = a 2 2 3 k ⟹
S ( a ) = 2 1 ( a 3 4 8 k 2 + a 6 + a 4 8 k 2 + 3 a 6 ) ⟹
d a d s = 2 a 2 4 8 k 2 + a 6 ( 2 3 + 6 ) a 6 − 4 8 k 2 ( 3 + 1 ) = 0 a = 0 ⟹ a = ( 8 3 k 2 ) 6 1 ⟹ h = ( 3 k ) 3 1
⟹ tan ( θ ) = a 2 h = 2 2 1 ∗ 3 4 1 ⟹ θ ≈ 6 1 . 7 5 1 5 3 0 ∘ and tan ( λ ) = 3 a 2 h = 3 4 1 2 2 1 ⟹ λ ≈ 4 7 . 0 5 8 5 9 7 ∘ ⟹ λ θ ≈ 1 . 3 1 2 2 2 6