Pyramids construction
The Pharaoh would like to cover the lateral sides of his square pyramid with the finest marble. In order to save the cost of construction, the builder tries to reduce the exposed surface area of the pyramid as much as possible.
What is the angle of inclination θ (in degrees) that minimizes the exposed surface area given a constant volume of the pyramid?
The answer is 54.7356.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
1st line: V= 1/3 a^2 h
You could have just used AM-GM instead of calculus.
Great problem.
If you calculate a couple more distances after finding h = 2 1 a , you discover that the faces of the pyramid are equilateral triangles. Call d the length of the shared edges of the triangles. h ′ d = h 2 + ( 2 1 a ) 2 = 2 1 a 2 + 4 1 a 2 = 2 3 a = h ′ 2 + ( 2 1 a ) 2 = 4 3 a 2 + 4 1 a 2 = a
Since the triangles are equilateral, the Pharoah's pyramid is the top half of a regular octahedron . And indeed, the dihedral angle (the angle formed by two faces) of a regular octahedron is 1 0 9 . 4 7 1 2 ∘ , exactly double the angle asked for in this problem.
Log in to reply
Using h' = root3/2a, sub that into the interior triangle, with base 1/2a. You will discover cos theta = 1/root 3. Inverse cos yields the correct answer. (sorry for the lack of mathematical figures on my phone keyboard)
Hi, why is the answer not 1/(infinity-1)? I.e have the shortest possible pyramid thus minimising the area of the sides to a value just slightly greater than the square base? What am I missing?
Log in to reply
A pyramid with zero height has no volume. If you keep the volume constant as you decrease the height h further and further, the base lenght a has to growth, so that in the limit h → 0 the base lenght (and, therefore, also the area) is infinitely large.
Using the diagram above:
Volume V = 3 1 a 2 h , where a = 2 h ′ cos θ , h = h ′ sin θ ⟹
V = 3 4 h ′ 3 cos 2 θ sin θ = K ⟹ h ′ = ( 4 cos 2 θ sin θ 3 K ) 3 1 ⟹
Lateral Surface Area S = 2 a h ′ ⟹ S ( θ ) = 4 h ′ 2 cos θ = j ( sec θ ) 3 1 ( csc θ ) 3 2 , where j is just a constant.
d θ d S = 3 j ( s e c θ ) 3 1 ( csc θ ) 3 2 ∗ ( tan θ − 2 cot θ ) = 0 ⟹
3 sin 2 θ − 2 = 0 ⟹ sin θ = ± 3 2 . choosing sin θ = 3 2 ⟹ θ = 5 4 . 7 3 5 6 ∘
Note: The angle θ is the same for any pyramid whose base is a regular n − g o n .
To show that angle θ is the same for any pyramid whose base is a regular n − g o n .
For area of n − g o n :
Let B C = x be a side of the n − g o n , A C = A B = r , A D = h ∗ , and ∠ B A D = n 1 8 0 .
2 x = r sin ( n 1 8 0 ) ⟹ r = 2 sin ( n 1 8 0 ) x ⟹ h ∗ = 2 x cot ( n 1 8 0 ) ⟹ A △ A B C = 4 1 cot ( n 1 8 0 ) x 2 ⟹
A n − g o n = 4 n cot ( n 1 8 0 ) x 2 ⟹ the Volume of the pyramid V p = 1 2 n cot ( n 1 8 0 ) x 2 H
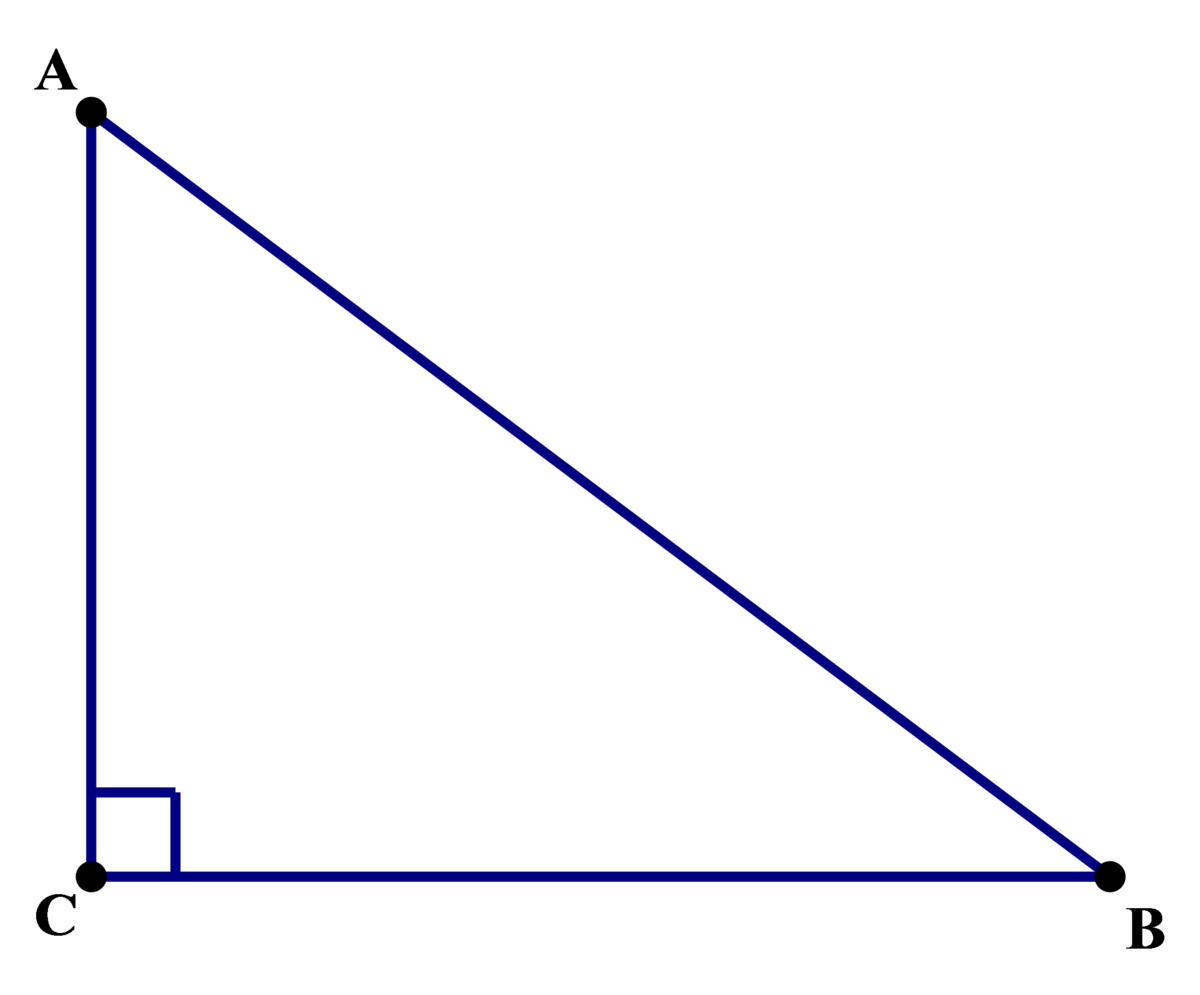
Let A C = H be the height of the pyramid, B C = h ∗ , and A B = h ′ be the slant height of the pyramid and m ∠ C B A = θ
The lateral surface area S = 2 n x h ′ .
h ∗ = 2 x cot ( n 1 8 0 ) = h ′ cos ( θ ) ⟹ x = 2 tan ( n 1 8 0 ) cos ( θ ) h ′ and H = h ′ sin ( θ ) and letting u ( n ) = tan ( n 1 8 0 ) ⟹ V p = 3 n u ( n ) cos 2 ( θ ) sin ( θ ) h ′ = K and S = n ∗ u ( n ) c o s ( θ ) h ′ 2 .
V p = 3 n u ( n ) cos 2 ( θ ) sin ( θ ) h ′ = K ⟹ h ′ = ( n ∗ u ( n ) c o s 2 ( θ ) s i n ( θ ) 3 K ) 3 1 ⟹ S ( θ ) = j ( n ) ∗ ( s e c ( θ ) ) 3 1 ( c s c ( θ ) ) 3 2 , where j ( n ) = ( 9 k 2 n ∗ u ( n ) ) 3 1
⟹ d θ d S = 3 j ( n ) ( s e c θ ) 3 1 ( csc θ ) 3 2 ∗ ( tan θ − 2 cot θ ) = 0 ⟹
3 sin 2 θ − 2 = 0 ⟹ sin θ = ± 3 2 . choosing sin θ = 3 2 ⟹ θ = 5 4 . 7 3 5 6 ∘
∴ The measure of the desired angle θ is independent of n .
You forgot the '2' in the first derivative line, 2*root(3V), but it does not affect the outcome.
Shouldn't you specify that we are dealing with a right pyramid?
How do we know that all outer triangles have the same area. They share common base but not necessarily a common height.
Log in to reply
Yes they do. If you imagine the right triangle drawn in the picture for every face, by Pythagorean theorem the heights of the triangular faces must be the same.
Log in to reply
No, not necessarily. Nowhere in the question does it say that we are dealing with a right pyramid.
1st line, a=cube root (3V/h) , not square root
Log in to reply
I corrected the typo, hopefully everything else is fine.
Let b = 2 1 a be half of the length of a side. The volume is proportional to V ∝ b 2 h . The area is proportional to A ∝ b h ′ ∝ b b 2 + h 2 ; in order to minimize the area, we might as well minimize its square, i.e. we minimize b 4 + b 2 h 2 . We wish to express this polynomial (of fourth degree) in terms of the constant V ∝ b 2 h (third degree) and the unknown t = tan θ = h / b (zeroeth degree). This must be done as follows: b 4 + b 2 h 2 ∝ V 4 / 3 ( t − 4 / 3 + t 2 / 3 ) . Thus we minimize the expression t − 4 / 3 + t 2 / 3 . The easiest way to do this is by setting the derivative equal to zero: 3 − 4 t − 7 / 3 + 3 2 t − 1 / 3 = 0 ; multiply by 2 3 t 7 / 3 : − 2 + t 2 = 0 . We find that tan θ = t = 2 , and so θ ≈ 5 4 . 7 3 5 6 ∘ .
Alternative
Since the volume is constant, we have (with t = tan θ = h / b ) 0 = d ( b 2 h ) = 2 b h d b + b 2 d h = b 2 ( 2 t d b + d h ) , so that d h = − 2 t d b .
To minimize the area we minimize b 4 + b 2 h 2 (see above); we set its total derivative equal to zero: 0 = d ( b 4 + b 2 h 2 ) = ( 4 b 3 + 2 b h 2 ) d b + 2 b 2 h d h = 2 b 3 [ ( 2 + t 2 ) d b + t d h ] ; substitute d h = − 2 t d b , we see that 0 = ( 2 + t 2 ) d b + t d h = ( 2 + t 2 − 2 t 2 ) d b = ( 2 − t 2 ) d b , from which t = 2 .
I love your solutions. They keep the brain engaged in a way that identifying an independent variable and 'cranking the handle' does not. I didn't understand immediately what you meant by 'degree' in this problem. Perhaps 'dimension' (in the way it is used in 'dimensional analysis') would be clearer?
But a great solution and thanks for posting.
Log in to reply
The degree of a monomial is the sum of the exponents. The degree of a polynomial is the maximum degree of its monomials. A polynomial is homogeneous is all monomials have the same degree.
Thus, b 4 + b 2 h 2 is homogeneous and of fourth degree, and b 2 h is homogeneous and of the third degree. By extending the concept, b / h = b 1 h − 1 is of zeroeth degree.
I used these concepts to arrive at the idea of taking a 4 / 3 power: ( degree four ) = A ⋅ ( degree three ) 4 / 3 ⋅ ( degree zero ) n .
I derived an equation for surface area in terms of theta only, then differentiated it, setting that to zero, getting tan theta = root 2; yielding the desired answer.
I wrote a python program to optimize the volume versus the top surface area using the functions
3V/a^2=h
,
hprime =a/cos(theta)
, and
SAtop=2*hprime*a
.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
|
Why not a² cover? Inverse pyramidal is just exposed by only this square fondation (only one of This lateral side exposed), no mater of angle (more than -45° dépend of budget) ... and cheapest solution for a poor Pharaon ! ;-)
My solution was similar to Rocco Dalto's. I'm just amazed at how close to 54 degrees the answer was, but that it wasn't actually 54 degrees. I was initially expecting a relationship to a golden angle.
Using a Golden Triangle of sides: height h = ϕ , base b = 1 and slant height s = ϕ , the angle made between the slant height and the base turned out to be cos − 1 ( 1 + 5 2 ) ~ 5 1 . 8 2 7 2 9 ∘ . Although the golden angle is ~ 1 3 7 . 5 0 7 7 6 ∘ which has nothing to do with the Golden Triangle(mine) or your triangle which has height h = ϕ , base b = 4 − ϕ 2 and slant height s = 2 . .
Log in to reply
I have to go for now, but I know 2 sin ( 5 4 ) = ϕ .
Log in to reply
Using a Golden Triangle of sides: height h = ϕ , base b = 1 and slant height s = ϕ , the angle made between the slant height and the base turned out to be cos − 1 ( 1 + 5 2 ) ~ 5 1 . 8 2 7 2 9 ∘ . Although the golden angle is ~ 1 3 7 . 5 0 7 7 6 ∘ which has nothing to do with the Golden Triangle(mine) or your triangle which has height h = ϕ , base b = 4 − ϕ 2 and slant height s = 2 . .
Using the diagram above:
Volume V = 3 1 a 2 h , where a = 2 h ′ cos θ , h = h ′ sin θ ⟹
V = 3 4 h ′ 3 cos 2 θ sin θ = K ⟹ h ′ = ( 4 cos 2 θ sin θ 3 K ) 3 1 ⟹
Lateral Surface Area S = 2 a h ′ ⟹ S ( θ ) = 4 h ′ 2 cos θ = j ( sec θ ) 3 1 ( csc θ ) 3 2 , where j is just a constant.
d θ d S = 3 j ( s e c θ ) 3 1 ( csc θ ) 3 2 ∗ ( tan θ − 2 cot θ ) = 0 ⟹
3 sin 2 θ − 2 = 0 ⟹ sin θ = ± 3 2 . choosing sin θ = 3 2 ⟹ θ = 5 4 . 7 3 5 6 ∘
Note: The angle θ is the same for any pyramid whose base is a regular n − g o n .
To show that angle θ is the same for any pyramid whose base is a regular n − g o n .
For area of n − g o n :
Let B C = x be a side of the n − g o n , A C = A B = r , A D = h ∗ , and ∠ B A D = n 1 8 0 .
2 x = r sin ( n 1 8 0 ) ⟹ r = 2 sin ( n 1 8 0 ) x ⟹ h ∗ = 2 x cot ( n 1 8 0 ) ⟹ A △ A B C = 4 1 cot ( n 1 8 0 ) x 2 ⟹
A n − g o n = 4 n cot ( n 1 8 0 ) x 2 ⟹ the Volume of the pyramid V p = 1 2 n cot ( n 1 8 0 ) x 2 H

Let A C = H be the height of the pyramid, B C = h ∗ , and A B = h ′ be the slant height of the pyramid and m ∠ C B A = θ
The lateral surface area S = 2 n x h ′ .
h ∗ = 2 x cot ( n 1 8 0 ) = h ′ cos ( θ ) ⟹ x = 2 tan ( n 1 8 0 ) cos ( θ ) h ′ and H = h ′ sin ( θ ) and letting u ( n ) = tan ( n 1 8 0 ) ⟹ V p = 3 n u ( n ) cos 2 ( θ ) sin ( θ ) h ′ = K and S = n ∗ u ( n ) c o s ( θ ) h ′ 2 .
V p = 3 n u ( n ) cos 2 ( θ ) sin ( θ ) h ′ = K ⟹ h ′ = ( n ∗ u ( n ) c o s 2 ( θ ) s i n ( θ ) 3 K ) 3 1 ⟹ S ( θ ) = j ( n ) ∗ ( s e c ( θ ) ) 3 1 ( c s c ( θ ) ) 3 2 , where j ( n ) = ( 9 k 2 n ∗ u ( n ) ) 3 1
⟹ d θ d S = 3 j ( n ) ( s e c θ ) 3 1 ( csc θ ) 3 2 ∗ ( tan θ − 2 cot θ ) = 0 ⟹
3 sin 2 θ − 2 = 0 ⟹ sin θ = ± 3 2 . choosing sin θ = 3 2 ⟹ θ = 5 4 . 7 3 5 6 ∘
∴ The measure of the desired angle θ is independent of n .
We consider the height h of the pyramid as a varyable parameter, whereas its side length a is fixed by the volume V = 3 1 a 2 h = const ⇒ a = h 3 V Pythagorean theorem yields the height h ′ of the triangular area h ′ = 4 a 2 + h 2 = 4 h 3 V + h 2 so that the total outer area (4 triangles) results to A = 4 ⋅ 2 1 a h ′ = 2 3 V 4 h 2 3 V + h In the minimum, the derivative must be zero ⇒ ⇒ ⇒ ∂ h ∂ A h 3 h θ = 3 V 4 h 2 3 V + h − 2 h 3 3 V + 1 = ! 0 = 2 3 V = 2 1 a 2 h = 2 1 a = arctan a 2 h = arctan 2 ≈ 5 4 . 7 3 5 6