Pythagoras' Slanting Sangaku
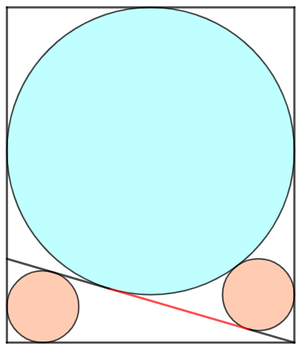
The diagram above illustrates a rectangle, containing two identical red circles and one cyan circle. Both cyan and red circles are tangent to the hypotenuse of the triangle whose incircle is a red circle. The length of the red segment formed by those two intersection points is 1 2 .
Input the area of the rectangle as your answer.
The answer is 672.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Label the figure as follows.
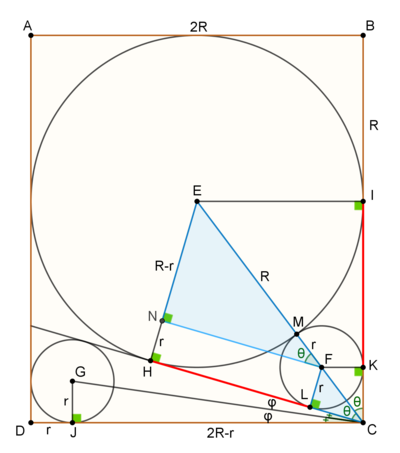 Denote by
R
the radius of the big circle and by
r
the radius of the small ones. Let
ϕ
=
∠
H
C
G
=
∠
G
C
J
and
θ
=
∠
F
C
K
=
∠
F
C
L
.
Denote by
R
the radius of the big circle and by
r
the radius of the small ones. Let
ϕ
=
∠
H
C
G
=
∠
G
C
J
and
θ
=
∠
F
C
K
=
∠
F
C
L
.
By Pythagoras’s theorem on right △ E F N ,
F N = E F 2 − E N 2 = ( R + r ) 2 − ( R − r ) 2 = 2 R r Hence,
2 R r = F N = I K = H L = 1 2 ⇒ R r = 3 6 ( 1 ) ∠ E F N and ∠ F C L are corresponding angles, thus, ∠ E F N = ∠ F C L = θ
On
△
E
N
F
,
tan
θ
=
N
F
E
N
=
1
2
R
−
r
(
2
)
On
△
G
C
J
,
tan
φ
=
J
C
G
J
=
2
R
−
r
r
(
3
)
Moreover,
2 θ + 2 φ = 9 0 ∘ ⇒ φ = 4 5 ∘ − θ ⇒ tan φ = tan ( 4 5 ∘ − θ ) = 1 + tan θ 1 − tan θ ⇒ ( 2 ) ( 3 ) 2 R − r r = 1 + 1 2 R − r 1 − 1 2 R − r ⇔ ( R − 1 2 ) ( R − r ) = 0 ⇒ R = r R = 1 2 From ( 1 ) we get r = 3 , hence, ( 2 ) ⇒ tan θ = 4 3 . On △ E I C ,
I C = tan θ E I = tan θ R = 4 3 1 2 = 1 6 Hence, for the dimentions of A B C D we have B C = B I + I C = R + I C = 1 2 + 1 6 = 2 8 and A B = 2 R = 2 4 Finally, for the area of the quadtrilateral, [ A B C D ] = A B ⋅ B C = 2 4 × 2 8 = 6 7 2
Label the rectangle A B C D , the right triangle A B E , circles centers O , P , and Q , O F and Q G perpendicular to B E , P H and P I are perpendicular to D A and A B , and Q J perpendicular to O F . Let the radii of the red circle and the blue circle be r and R respectively.
Then the red segment F G = Q J = O Q 2 − O J 2 = ( R + r ) 2 − ( R − r ) 2 = 2 r R = 1 2 ⟹ r R = 3 6 . Let ∠ A B E = θ . Then
A B 2 R 2 r R ⟹ r 2 = A I + I B = r + r cot 2 θ = r 2 + t r 2 = 1 + t 7 2 t Let t = tan 2 θ Note that r R = 3 6
And
B E A B ⋅ sec θ cos θ 2 R 2 R ⋅ 1 − t 2 1 + t 2 7 2 ⋅ 1 − t 2 1 + t 2 7 2 ⋅ 1 − t 2 1 + t 2 1 − t 2 6 + 6 t 2 ⟹ r = B G + F G + E F = r cot ( 2 9 0 ∘ − θ ) + 1 2 + R cot ( 2 9 0 ∘ + θ ) = r cot ( 4 5 ∘ − 2 θ ) + 1 2 + R cot ( 4 5 ∘ + 2 θ ) = r ⋅ 1 − t 1 + t + 1 2 + R ⋅ 1 + t 1 − t = 1 − t 1 + t ⋅ r 2 + 1 2 r + 3 6 ⋅ 1 + t 1 − t = 1 − t 1 + t ⋅ 1 + t 7 2 t + 1 2 r + 3 6 ⋅ 1 + t 1 − t = 1 − t 6 t + r + 1 + t 3 − 3 t = 1 − t 2 3 ( 1 − t 2 ) = 3 Multiply both sides by r Note that r R = 3 6 and r 2 = 1 + t 7 2 t
From r 2 = 1 + t 7 2 t ⟹ t = 7 1 , R = r 3 6 = 1 2 , B C = r cot ( 4 5 ∘ − 2 θ ) + 1 2 + R = 3 ⋅ 1 − 7 1 1 + 7 1 + 1 2 + 1 2 = 2 8 , and the area of the rectangle A B ⋅ B C = 2 ⋅ 1 2 ⋅ 2 8 = 6 7 2 .