Pythagoras's Dark Secret

Geometry Level 3

On the picture above, area of square $ABDE$ , $CAFG$ and $BCHK$ are 25, 16 and 9, respectively. Find the area of the shaded region (in $\text{unit}^2$ ).

The answer is 20.5.

3 solutions

Jason Chrysoprase
Oct 1, 2016

From the figure above, we know that $AB=5$ , $BC=3$ and $AC=4$ , so

$[AFGB] = \dfrac{(4+7)\times 4}{2} = \dfrac{44}{2}$

$[BGF] = \dfrac{7 \times 4}{2} = \dfrac{28}{2}$

$[ABD]= \dfrac{[ABDE]}{2} = \dfrac{25}{2}$

Let’s assume that $A$ is the shaded area, thus

$A=[ABD]+[AFGB]-[BGF]=\dfrac{25+44-28}{2}=\dfrac{41}{2}=20.5$

Thanks Jason

Joy Patel - 4 years, 8 months ago

ar(ABD)=25/2=12.5 AD=5√2 ,if we a perpendicular from B to AD then bisects it lets say at M AM=(5√2)/2=5/√2 AB^2=AM^2+BM^2 25=25/2+BM^2 BM=5/√2 ar(AFB)=1/2.b.h=1/2.4.BM=2.5/√2=5√2 Area of shaded figure=ar(ABD)+ar(AFB)=12.5+5√2 =19.57 cm^2 I don't see any mistake in this approach if you then please share it

Joy Patel - 4 years, 8 months ago

I see you assume that $FA$ and $AD$ in one line. No they are not.

Jason Chrysoprase - 4 years, 8 months ago

Marta Reece
Mar 10, 2017

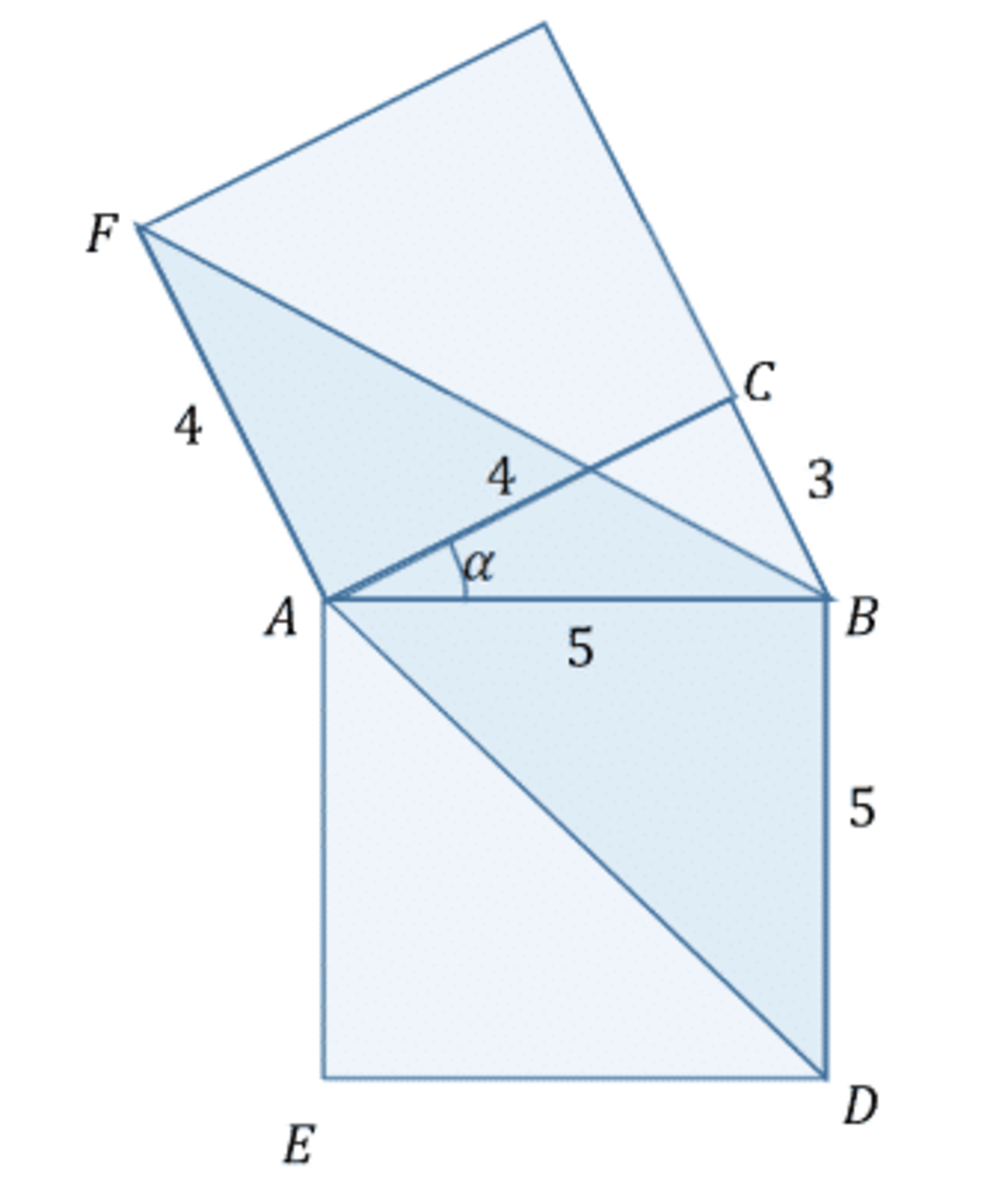
Triangle $ABD$ has area $\frac{25}{2}$ .

Angle $\alpha=arccos(\frac{4}{5})$ .

Area of $\triangle ABF=\frac{1}{2}\times 4\times 5\times sin(90^\circ+\alpha)=10\times cos(\alpha)=10\times \frac{4}{5}=8.$

Vishwash Kumar Γξω
Oct 5, 2016

Pythagoras's Dark Secret

The answer is 20.5.

3 solutions

0 pending reports