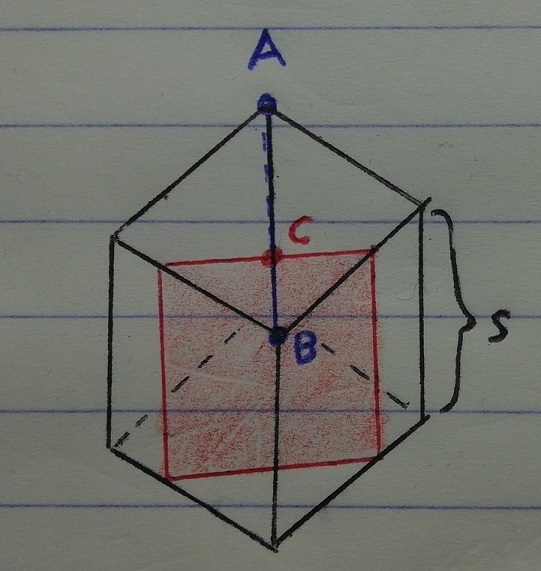
Pythagorean Cross Section

Let the side of the cube be $s$ . Since $BC$ is the same as half a side, $BC = \frac{1}{2}s$ , and since $AB$ is the diagonal of a square with side $s$ , $AB = \sqrt{2}s$ . Therefore, the ratio $\frac{BC}{AC} = \frac{\frac{1}{2}s}{\sqrt{2}s} = \boxed{\frac{\sqrt{2}}{4}}$ .

We're trying to find $\frac{\overline{BC}}{\overline{AB}}$ , so let's find $\overline{AB}$ first. We can call the side of the cube $s$ . Using the pythagorean theorem, we know that: $s^2+s^2=(\overline{AB})^2\implies{2s^2=(\overline{AB})^2}\implies{\sqrt{2}s=\overline{AB}}$ So we have our answer for $\overline{AB}$ in terms of $s$ . Now onto $\overline{BC}$ . Let's illustrate the top face of the cube and label a couple things to make notation easier. 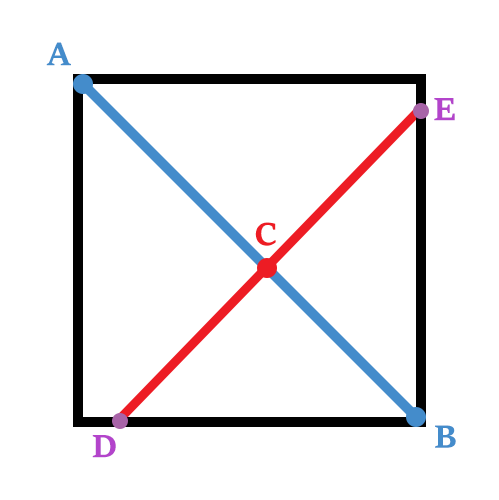The distance from the top side of the cross section (that is, $\overline{DE}$ ) to $B$ should be such that the whole cross section's area is equal to the face of the cube. Since the cross section is completely vertical, that can only happen when $\overline{DE}=s$ . And since $\overline{DE}$ is perpendicular to $\overline{AB}$ , $\overline{DB}$ and $\overline{BE}$ must be equal. Let's call them both $t$ for simplicity. 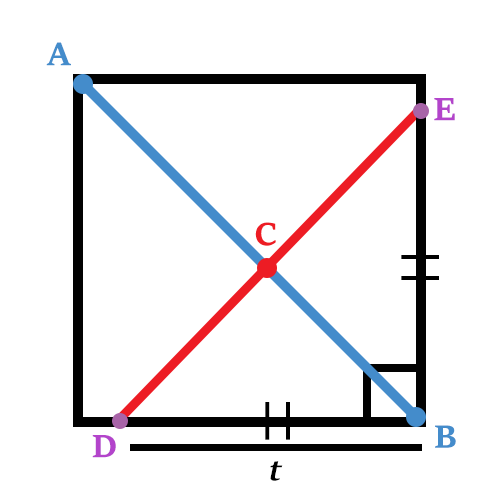But what is $t$ ? Notice $t$ is the side of a right triangle with hypotenuse $s$ . We can use the pythagorean theorem again to find $t$ in terms of $s$ . $t^2+t^2=s^2\implies{2t^2=s^2}\implies{\sqrt{2}t=s}\implies{t=\frac{\sqrt{2}s}{2}}$ Notice that $\overline{BC}$ is part of a $t$ -sided right triangle, more specifically, $\overline{BC}$ is the height of the right traingle. And since $\overline{BC}$ is perpendicular to $\overline{DE}$ we can use the inverse pythagorean theorem and substitute $t$ to find $\overline{BC}$ : $\frac{1}{t^{2}}+\frac{1}{t^{2}}=\frac{1}{(\overline{BC})^2}\implies{\frac{1}{\Big(\frac{\sqrt{2}s}{2}\Big)^2}+\frac{1}{\Big(\frac{\sqrt{2}s}{2}\Big)^2}=\frac{1}{\big(\overline{BC}\big)^2}}$ $\frac{1}{\Big(\frac{2s^2}{4}\Big)}+\frac{1}{\Big(\frac{2s^2}{4}\Big)}=\frac{1}{\big(\overline{BC}\big)^2}\implies{\frac{4}{2s^2}+\frac{4}{2s^2}=\frac{1}{\big(\overline{BC}\big)^2}}\implies{\frac{8}{2s^2}=\frac{4}{s^2}=\frac{1}{\big(\overline{BC}\big)^2}}$ $\frac{s^2}{4}=\big(\overline{BC}\big)^2\implies{\frac{s}{2}=\overline{BC}}$ Now that we have both $\overline{AB}=\sqrt{2}s$ and $\overline{BC}=\frac{s}{2}$ it's time to find $\frac{\overline{BC}}{\overline{AB}}$ . $\frac{\overline{BC}}{\overline{AB}}=\frac{\frac{s}{2}}{\sqrt{2}s}=\frac{s}{2}\times\frac{1}{\sqrt{2}s}=\frac{s}{2\sqrt{2}s}=\frac{\sqrt{2}s}{4s}=\boxed{\frac{\sqrt{2}}{4}}$ Not the most elegant or efficient solution, I know. This problem came to mind and this is how I solved it. I'm excited to see your own solutions!

AB = s sqrt(2). (BC)^2 = (S/sqrt(2))^2 - (S/2)^2 = S^2/2 - S^2/4 = S^2/4, so BC =S/2. Then CB/AB = (S/2)/(S sqrt(2) = 1/(2*sqrt(2)) = sqrt(2)/4.