Pythagorean Riddle

Geometry Level 5

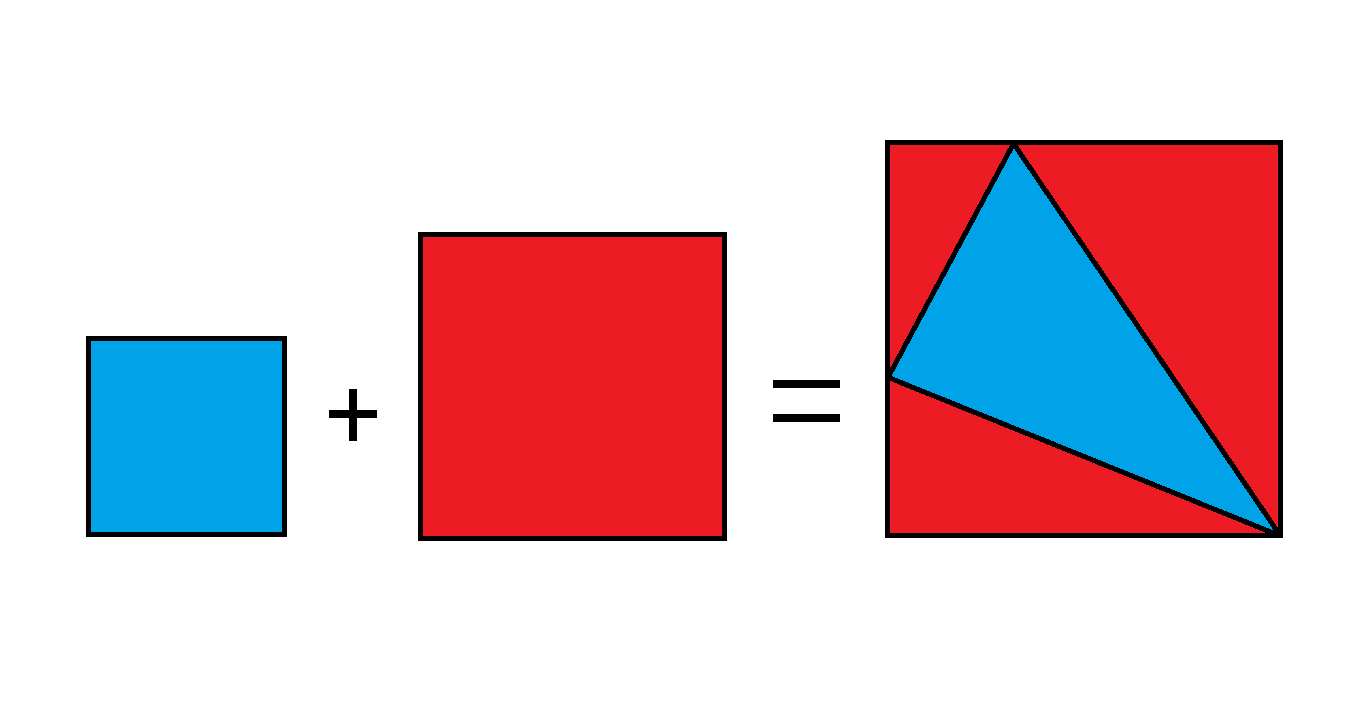
The equation above shows that the sum of the areas of the blue and red squares on the left side is equal to the area of the big square on the right side. In addition, the area of the blue square equals the area of the blue triangle, and the area of the red square equals the combined area of the 3 red triangles. Each of the three squares has an integer side length.

If the 2 vertices of the blue triangle each divide the corresponding sides on which they lie into smaller integer lengths, what is the least possible difference between the red square's area and the blue square's area?

The answer is 28.

2 solutions

Worranat Pakornrat
Feb 23, 2017

Relevant wiki: Pythagorean Triples

Let the side lengths of the blue, red, and biggest square be $a, b, c$ respectively. It is obvious that they make up a Pythagorean triple :

$a^2 + b^2 = c^2$

Now if we let $x$ & $y$ be the side lengths as shown above, we can calculate the red area $b^2$ :

$b^2 = \dfrac{1}{2}(cx + cy +(c-x)(c-y)) = \dfrac{c^2 + xy}{2}$

$2b^2 = c^2 +xy$

$xy = 2b^2 - c^2 = b^2 - a^2 = (b+a)(b-a)$

To find the least area difference, we will need the least possible Pythagorean triple. The first would be $5^2 = 4^2 + 3^2$ though $4^2 - 3^2 = 7$ , and $7$ is prime, making either $x$ or $y$ to be $7$ , which exceeds the square length of $5$ , which is inapplicable.

Then we shift to the next least triple: $10^2 = 8^2 + 6^2$ , and $8^2 - 6^2 = 28$ .

By letting $x=4$ and $y=7$ , all constraints are followed:

$8^2 = \dfrac{1}{2}(40 + 70 +(10-4)(10-7)) = 64$ .

Thus, the solution is $\boxed{28}$ .

Nice problem and solution. As far as I can tell, the only such Pythagorean triples that work are of the form $(3k, 4k, 5k)$ for $k \ge 2$ . For $k = 3$ there is one possible configuration $(x,y) = (7,9)$ , and for $k = 4$ there are two possible configurations, namely $(8,14)$ and $(7,16)$ . For $k = 5$ there is just $(x,y) = (7,25)$ , which has the blue triangle with its base of length $18$ coinciding with the side of the big square. For $k = 6$ there are three configurations: $(x,y) = (9,28), (12,21), (14,18)$ .

For this family of solutions we are needing to factor $16k^{2} - 9k^{2} = 7k^{2}$ in pairs in such a way that each factor in the pair is $\le 5k$ . The first value $k \ge 2$ for which we cannot do this is $k = 7$ .

Brian Charlesworth - 4 years, 3 months ago

I agree with your theory. I also tried to calculate other Pythagorean triples, but all seemed to result in big primes longer than the biggest square, thus ending up with primitive 3,4,5 triple.

Worranat Pakornrat - 4 years, 3 months ago

Niranjan Khanderia
Mar 1, 2017

Pythagorean Riddle

The answer is 28.

2 solutions

0 pending reports