Pythagorean Theorem again......

Algebra Level 2

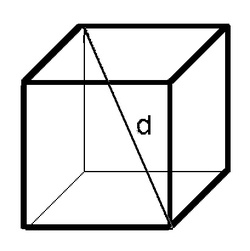What is the length of each diagonal of a cube that is 45 cm on each side? Round your answer to the nearest hundredth please.

The answer is 77.94.

3 solutions

Melissa Quail
Dec 29, 2014

Using 3D Pythagoras, the length of the 3D diagonal will be equal to the square root of the sum of the squares of the length, depth and height. So D = $\sqrt{45^{2}+45^{2}+45^{2}}$ = 77.94 cm.

A Former Brilliant Member
Oct 27, 2017

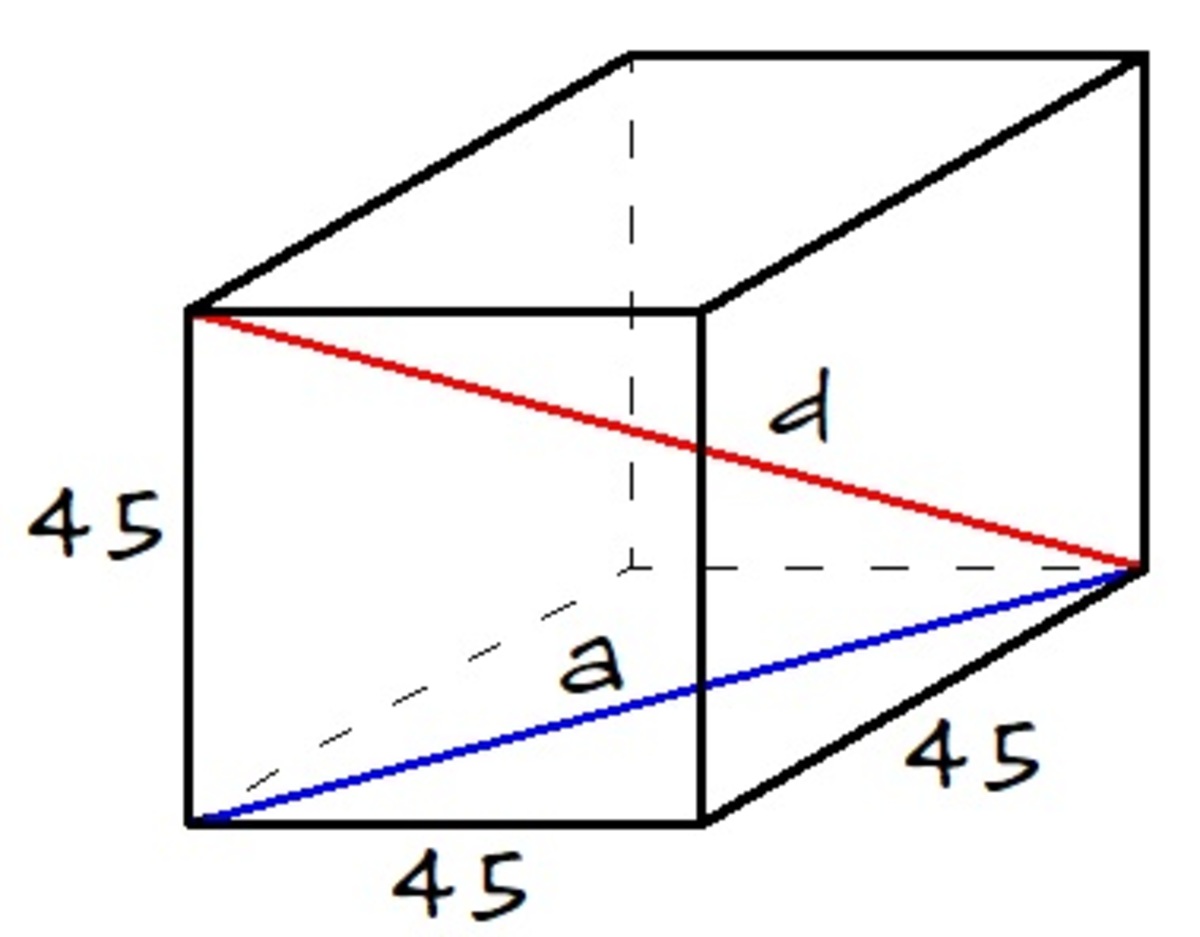Let $a$ be the face diagonal and $d$ be the space diagonal.

By pythagorean theorem, we have

$a=\sqrt{45^2+45^2}=45\sqrt{2}$

By pythagorean theorem again, we have

$d=\sqrt{a^2+45^2}=\sqrt{(45\sqrt{2})^2+2025}=\sqrt{6075} \approx$ $\boxed{77.94}$

Robert Fritz
Apr 25, 2014

I used the Pythagorean theorem....... Yep. First pictured it in your head. Realize that one of the legs instantly has a length of 45 cm. The next is the diagonal of a side of the cube so the hypotenuse which using the theorem comes out to be about 63.64 cm. Then use the theorem one last time and get 77.94. If you didn't have a calculator or paper or both, this might have been a bit of a time consuming problem. Thanks for using your time to answer 😀

We do not need to find the length of diagonal of one side in decimal form, because,

$d^2$ = 2 $a^2$ ,

where d is the diagonal of one of the face of cube and a is the side length. Let D be the length of each diagonal of the cube.

$D^2$ = $d^2$ + $a^2$

$D^2$ = 2 $a^2$ + $a^2$

$D^2$ = 3 $a^2$

D = 45 $\sqrt3$

D = [ $45 \times 1.732$ ] [Assuming value of $\sqrt3$ as 1.732]

Therefore, D = 77.94

Arpit Sah - 7 years, 1 month ago

Huh.... Never new that. Nice one!

Robert Fritz - 7 years, 1 month ago

Pythagorean Theorem again......

The answer is 77.94.

3 solutions

0 pending reports