Pythagorean theorem#2
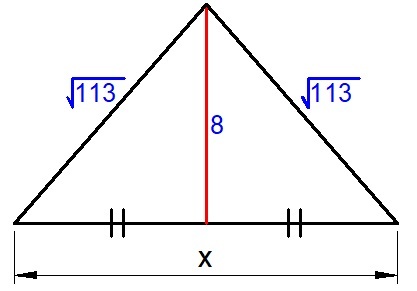
Below is an isosceles triangle. Find the length of the base, x .
The answer is 14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Nice solution
First name the triangle,then apply apollonius theorem to the triangle. the side which is bisecting the base is median so,(side)^2+(side)^2=2( median^2 + half of base^2 ) Using Apollonius theorem, you will be able to find the base.
I think this will be helpful
 x
=
2
(
1
1
3
)
2
−
8
2
=
2
1
1
3
−
6
4
=
2
4
9
=
2
(
7
)
=
1
4
x
=
2
(
1
1
3
)
2
−
8
2
=
2
1
1
3
−
6
4
=
2
4
9
=
2
(
7
)
=
1
4
Relevant wiki: Pythagorean Theorem
Suppose, thee sides of the triangle is a , b , and c . So we can use Pythagorean theorem .
Here a = ? , b = 8 and c = 1 1 3
Now,
a 2 + b 2 = c 2
⇒ a 2 + 8 2 = ( 1 1 3 ) 2
⇒ a 2 + 6 4 = 1 1 3
⇒ a 2 = 1 1 3 − 6 4
⇒ a = 4 9
Hence a = 7
Since a = 7 and a is half of the length of x , we can multiply to find x
x = a × 2
Hence x = 7 × 2 = 1 4