QAM Modulation

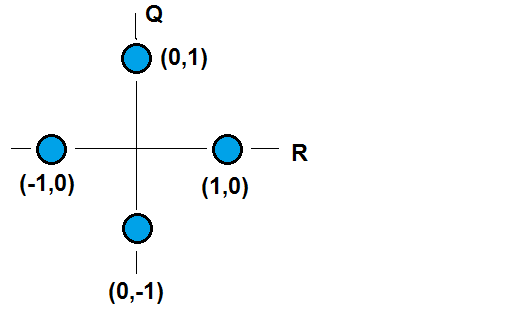
In a "Quadrature Amplitude Modulation" communication scheme, binary states are encoded using weighted sums of sine and cosine waves. Consider the following idealized message signal:

$M(t) = R \, cos(\omega t) + Q \, sin(\omega t)$

The message signal consists of a "reference" sinusoid with weight $R$ , and a "quadrature" sinusoid with weight $Q$ . The constellation above shows four states, corresponding to 2 bits per symbol (a unique 2-bit binary state for each allowed configuration of $M(t)$ ).

Suppose the actual signal $M'(t)$ consists of the ideal signal $M(t)$ combined with an error signal $E(t)$ (due to channel noise, etc.):

$M'(t) = M(t) + E(t) \\ = (R + \Delta R) \, cos(\omega t) + (Q + \Delta Q) \, sin(\omega t)$

Define "signal energy" as the Euclidean norm of the reference and quadrature components. Assume that a noisy symbol will be misinterpreted by the receiver if it is closer (distance-wise) to another symbol in the constellation, than to the intended symbol. Given the QAM constellation above, what minimum error signal energy will cause the receiver to misinterpret a QAM symbol?