Geometry is fun
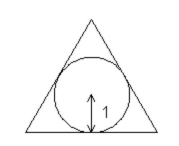
An equilateral triangle is circumscribed, find the area of the triangle
Give your answer to 3 decimal places.
The answer is 5.1961524227066319.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
How did you get BC and AM?
Log in to reply
Ritu, sorry, I didn't explain it clearly. Sorry also B C = tan 3 0 ∘ 2 . Thanks for your questions, I have edited the solution.
We note that ∠ O B C = 3 0 ∘ . Let the radius of the incircle be r = 1 . Then B M r = tan 3 0 ∘ ⇒ B M = tan 3 0 ∘ r and B C = 2 B M = 2 × tan 3 0 ∘ r = 2 × 3 1 1 = 2 3 .
Again, ∠ O A B = 3 0 ∘ and A M = A O + O M , O M = r = 1 and A O r = sin 3 0 ∘ ⇒ A O = sin 3 0 ∘ r = sin 3 0 ∘ 1 . Therefore, A M = 1 + sin 3 0 ∘ 1 .
You can divide the triangle into 6 congruent 30-60-90 triangles. 1 being the side opposite to the 30 degree angle. Hence, the base of the smaller triangle will be sqrt(3). Using this, we can find the area of the smaller triangle, [1xsqrt(3)]/2=0.866~. We multiply the area by 6, since we divided the triangle into 6 congruent parts, getting the answer 6x0.866=5.196.
If we add the top of the triangle with the center of the circle we will get another triangle there.In this case we know that the hypotenuse is twice the radius . The radius of the circle is 1 so, the hypotenuse is 2 × 1 now use the theorem of the pithagoras x 2 + 1 2 = 2 2 ;[Base=x] so, x= 3 now, the length of equilateral triangle is 2 × x so, 2 × 3 =3.46) here a=3.46 ;[a is the length of the equilateral triangle] now, we know the formula of the area of equilateral triangle
by calculating we will get the area of the equilateral triangle so, the answer is 5.2
Let the triangle be △ A B C , A being at the top, B C the base, and the center of the unit radius incircle be O . Then A O , B O and C O divide internally the ∠ A , ∠ B and ∠ C respectively. Let the incircle touches B C at M . Due to symmetry, M is the midpoint of B C .
The area of the triangle = 2 1 × B C × A M
= 2 1 ( 2 × B M ) ( A O + O M )
= 2 1 ( 2 × tan 3 0 ∘ 1 ) ( 1 + sin 3 0 ∘ 1 )
= 2 1 ( 3 1 2 ) ( 1 + 2 1 1 )
= 2 1 ( 2 3 ) ( 1 + 2 ) = 3 3 ≈ 5 . 1 9 6