Quadrants touching a circle in a square
Geometry
Level
2
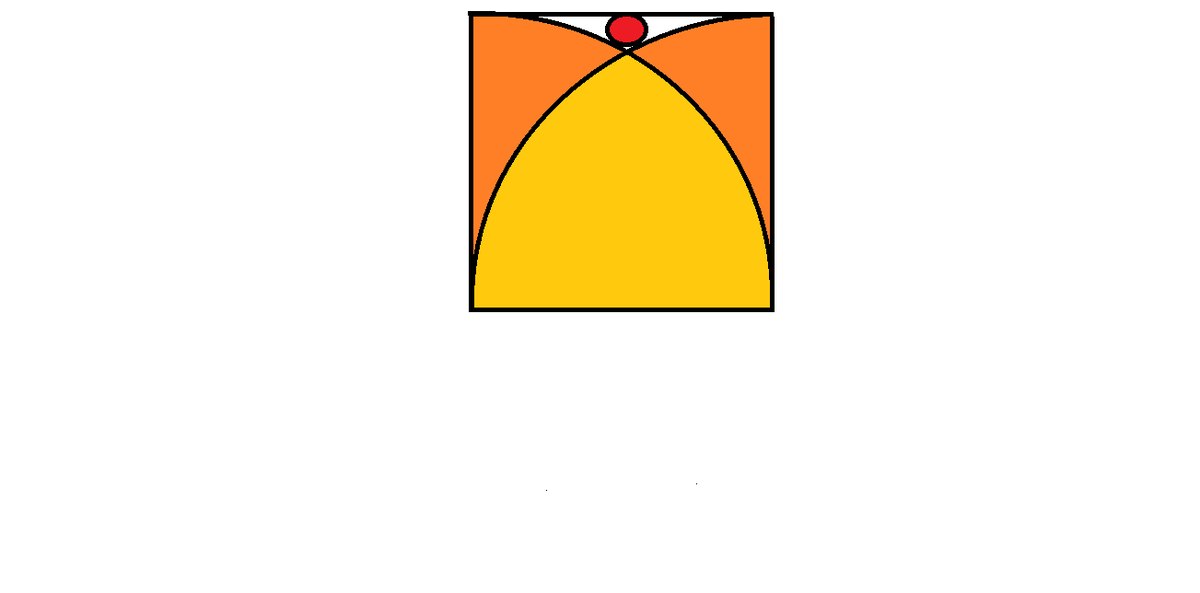
Given a square having a side of length 32 units, find the radius of the small red circle at the top, which barely just touches the two quadrants.
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Nice, fun problem!
Let r be the radius of the red circle with center C . Consider the right triangle with its vertices at C , the left lower corner, and the midpoint of the lower edge. Pythagoras gives us ( 3 2 + r ) 2 = 1 6 2 + ( 3 2 − r ) 2 , which solves to r = 2 .