Near Twin Radicals

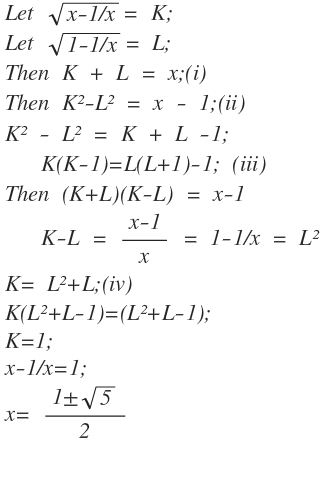
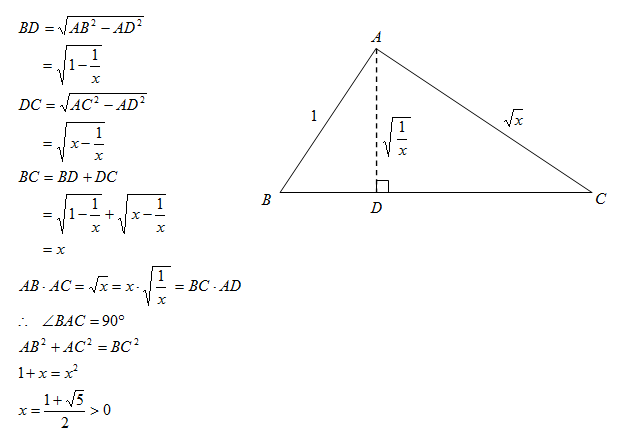
Since we're dealing with radicals, let's square both sides of the equation in hopes of converting the radical equation into a polynomial equation, which is easier to solve.

By squaring the equation in question, (recall that $(a+b)^2=a^2+b^2+2ab$ ), we have

$\begin{aligned} \left( x- \dfrac1x\right) + \left( 1 - \dfrac1x \right) + 2 \sqrt{ \left( x - \dfrac1x \right) \left( 1 - \dfrac1x \right)} &=& x^2 \\ x^2 + x -2 + 2 \sqrt{(x^2-1)(x-1)} &= & x^3 \\ \left( 2 \sqrt{(x^2-1)(x-1)} \right)^2 &= & (x^3 -x^2 - x + 2)^2 \\ 4(x^2-1)(x-1) &=& (x^3 -x^2 - x + 2)^2 \\ x^6 -2x^5 - x^4+2x^3+x^2 &=& 0 \\ (x^3 +x^2 + x)^2 &=& 0 \\ x(x^2-x - 1) &=& 0 \\ x &=& 0, \dfrac{1\pm \;\sqrt5}2 \qquad \text{ by Quadratic formula} \end{aligned}$

But substituting all these three values of $x$ into the original equation shows that $x=0$ and $x = \dfrac{1-\sqrt5}2$ are extraneous roots (they do not satisfy the given equation). Thus the solution of $x$ satisfying the equation in question is $\boxed{ \dfrac{1+\sqrt5}2 }$ .