Quadratic Inequality with a given solution set

For any given $n$ the quadratic inequality $-x^2 + 2nx - n^2 \geq 0$ has a solution set consisting of only the number $n$ . So $L = \{n\}$ . Example $n = 3$ then the inequality becomes: $-x^2 + 6x - 9 \geq 0$ using the quadratic formula we get: ${x = \frac{{ - 6 \pm \sqrt {36 - 4 \times -1 \times 9} }}{{-2}}}$ , which simplifies to x = ${x = \frac{{ - 6 }}{{-2}}} = 3$ . The fact that $a < 0$ has to be true becomes clear if we graph a quadratic function: $a < 0$ has to be true in order for the function to be closed at the top otherwise the inequality $ax^2 + bx + c \geq 0$ could not have only one single solution.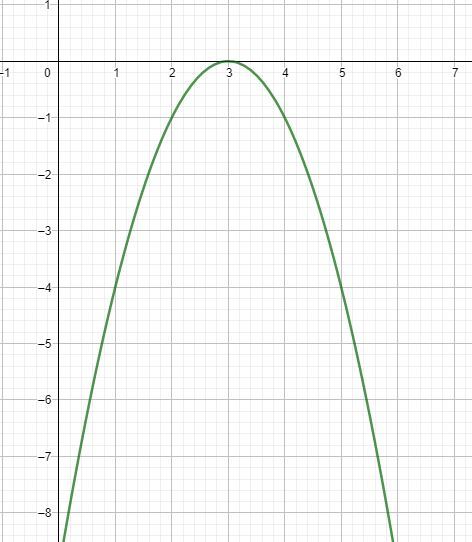 For the other coefficients let's recall that a quadratic equation only consists of one solution if $D = b^2 -4ac = 0$ so if we plug in our values: $4n^2 - 4 \times -1 \times - n^2 = 0$ $= 4n^2 - 4n^2 = 0$ . So $a = -1$ , $b = 2n$ and $c = -n^2$ is the only given combination that works in this case.