Quadratic Inequality
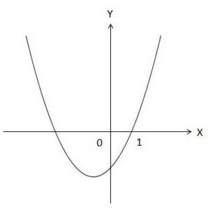 The graph above is a quadratic function,
for some constant
. What is the solution to the quadratic inequality
?
The graph above is a quadratic function,
for some constant
. What is the solution to the quadratic inequality
?
Clarification: The graph intersects the -axis at .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
As x = 1 is solution to the ecuation we can replace the point ( 1 , 0 ) in the parabole, where we get k = 1 , so the parabola gets y = ( x − 1 ) ( x + 2 ) and the interval where the parabola gets negative is ( − 2 , 1 )