Quadriangles...

Geometry Level 2

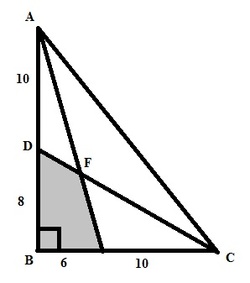Given that A B ‾ ⊥ B C ‾ \overline { AB } \bot \overline { BC } , BD=8, BE=6, AD=10 and CE=10, find the area of quadrilateral DBEF.

34 square units 30 square units 35 square units 33 square units

View wiki
Mark Vincent Mamigo by Mark Vincent Mamigo , 24, Philippines

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

6 solutions

Ajit Athle
Oct 9, 2014

Drop a perpendicular from F to BC, say FX. F can be determined as (4,6) from the eqns.: x/6 + y/18 = 1 and x/16 + y/8=1. Thus, FX = 6 units.
Area DBEF = Tr. ABC - Tr. ADC - Tr. FEC = 18x8 -10x8 -10x3 = 34 Sq. Units

11 Helpful 0 Interesting 0 Brilliant 0 Confused

1.draw perpendicular f to bc say fx. 2.find the coordinates of f=(4,6). 3.it means fx=6,that means area fec=1/2 * ec * fx=30 4.area dbc=1/2 * db * bc=64 5.area dbef=64-30=34

Shekhar Pal - 6 years, 8 months ago

how will the both BE and FX are equal

Mahesh Perumandla - 6 years, 8 months ago

  1. First of all, let E be the meeting point of BC and the extension of AF.
  2. Join D and E to obtain DE. Let DE = a. By Pythagorean Theorem: DE = sqrt(DE^2+DB^2) = sqrt (8^2+6^2) = 10.
  3. Area of quadrilateral DFEB = area of triangle DBE + area of triangle DFE.
  4. Area of triangle DFE can be found out by Heron’s or Hero’s formula.
  5. Again, by Pythagorean theorem, AE = sqrt(18^2+6^2) = 6 sqrt(10). AC = sqrt(18^2+16^2) = 2 sqrt(145). DC = sqrt(8^2+16^2) = 8*sqrt(5).
  6. Since AD = DE = EC = 10, triangle ADE and triangle DEC are isosceles triangles. Hence, angle DAF = angle DEF and angle EDF = angle ECF.
  7. Now, angle FCE = cos inverse (16/(8 sqrt(5))) = cos inverse (2/sqrt(5)) = angle FDE and angle DAF = cos inverse (18/(6 sqrt(10))) = cos inverse (3/sqrt(10)) = angle FED.
  8. Thus, angle AEB = 180 – (90+cos inverse (3/sqrt(10))) = 71.56505118 degrees.
  9. Similarly, angle BDC = 180-(90+cos inverse (2/sqrt(5))) = 63.43494882 degrees.
  10. Thus, angle DFE = 360-(90+angle BDC+angle AEB) = 360-(90+63.43494882+71.56505118) = 135 degrees.
  11. By using sine law or sine rule or sine formula or law of sines to triangle DFE; (DF/(sin(cos inverse (3/sqrt(10)))))=(FE/(sin(cos inverse(2/sqrt(5)))))=(DE/sin(135). DE being 10, DF and FE can be found out.
  12. DF = b = 4.472135955 and FE = c = 6.32455532 with DE = 10 = a.
  13. Now, applying Heron’s formula or Hero’s formula to triangle DFE: s=(a+b+c)/2 = 10.39834564. Area of triangle DFE = sqrt(s (s-a) (s-b)*(s-c)) = 9.99999998 ~= 10.
  14. Finally, area of quadrilateral DFEB = area of triangle DBE + area of triangle DFE = (1/2) 8 6 + 10 = 34.

Suhas Dinesh - 6 years, 8 months ago

Log in to reply

Bro just use similar triangles..no need of using herons formula or any other complicated trigo function

Shyam Kumar - 6 years, 8 months ago

Here the line drawn from F does'nt seem to be pependicular

sandeep Rathod - 6 years, 6 months ago
Al Dziivraa
Oct 10, 2014

A(0,18) , B(0,0) , C(16,0) , D(0,8) , E(6,0).

CD slope is -1/2 , AE slope is -3.

equation for CD is x+2y=16 & eq. for AE is 3x+y=18.

then the equations tell that F coordinate is (4,6).

Area EBDF=1/2 [(XbYe + XdYb + XfYd + XeYf )-(XeYb + XbYd + XdYf + XfYe )]=34 sq. units.

5 Helpful 0 Interesting 0 Brilliant 0 Confused

we can use the principle of similar triangles to solve this problem..from the point F draw perpendiculars to AB and BC..label the points as P and Q respectively..use the similarity of triangles AFP with ABE and triangle CFQ with CBD..find out the required lengths...now the quad can be split into two triangles and a rectangle..the sum of the areas being(6+4+24=34)

Shyam Kumar - 6 years, 8 months ago
James Villanueva
Oct 10, 2014

i ) i) Draw a perperdicular segment from F F to B C ‾ \overline { BC } and let G G be their point of intersection. Δ A B E ΔABE and Δ F G E ΔFGE are similar triangles, so F G = 3 ⋅ G E FG=3 \cdot GE ; In addition, Δ D B C ΔDBC and Δ F G C ΔFGC are also similar triangles, so 2 ⋅ F G = G E + 10 u 2 \cdot FG = GE+10u ; solving that system of equations, we get F G = 6 u FG=6u and G E = 2 u GE=2u .

i i ) ii) By looking at the drawing:

A r e a B D F E = A r e a Δ D B C − A r e a Δ F E C Area BDFE = AreaΔDBC - AreaΔFEC

A r e a B D F E = ( D B ) ( B C ) 2 − ( F G ) ( E C ) 2 Area BDFE = \frac { (DB)(BC) }{ 2 } - \frac { (FG)(EC) }{ 2 }

A r e a B D F E = ( 8 u ) ( 16 u ) 2 − ( 6 u ) ( 10 u ) 2 Area BDFE = \frac { (8u)(16u) }{ 2 } - \frac { (6u)(10u) }{ 2 }

A r e a B D F E = 34 u 2 Area BDFE = 34u^{2}

3 Helpful 0 Interesting 0 Brilliant 0 Confused
Venture Hi
Oct 21, 2014

Use analytic geometry. Equation AE= > y=-3x+18 and Equation DC=>y= -1/2x+8. Find the intersecting point which is (4,6) Then just calculate the two small triangles and rectangle= 4+24+6=34

2 Helpful 0 Interesting 0 Brilliant 0 Confused

I'm sorry if i forgot to put an "E" between B and C..

0 Helpful 0 Interesting 0 Brilliant 0 Confused

Alternative approach:

Let α ( P ) \alpha(P) denote the area of a polygon P P and let h h denote the height (from F F ) of Δ F E C \Delta FEC .

Clearly α ( D B C ) = 1 2 ⋅ 16 ⋅ 8 = 64 \alpha( DBC) = \frac{1}{2} \cdot 16 \cdot 8 = 64 and α ( F E C ) = 1 2 ⋅ 10 ⋅ h \alpha(FEC) = \frac{1}{2} \cdot 10 \cdot h .

Since 5 ⋅ h = 64 − α ( D B E F ) 5\cdot h = 64 - \alpha(DBEF) , the area of Δ F E C \Delta FEC must be a multiple of 5 (i.e. the last digit must be 0 or 5). Among our choices, that is only true when α ( D B E F ) \alpha(DBEF) = 34.

Note: Without the multiple choices, a little more work using the approach above would solve the problem as well.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...