Quadrilateral Incircle
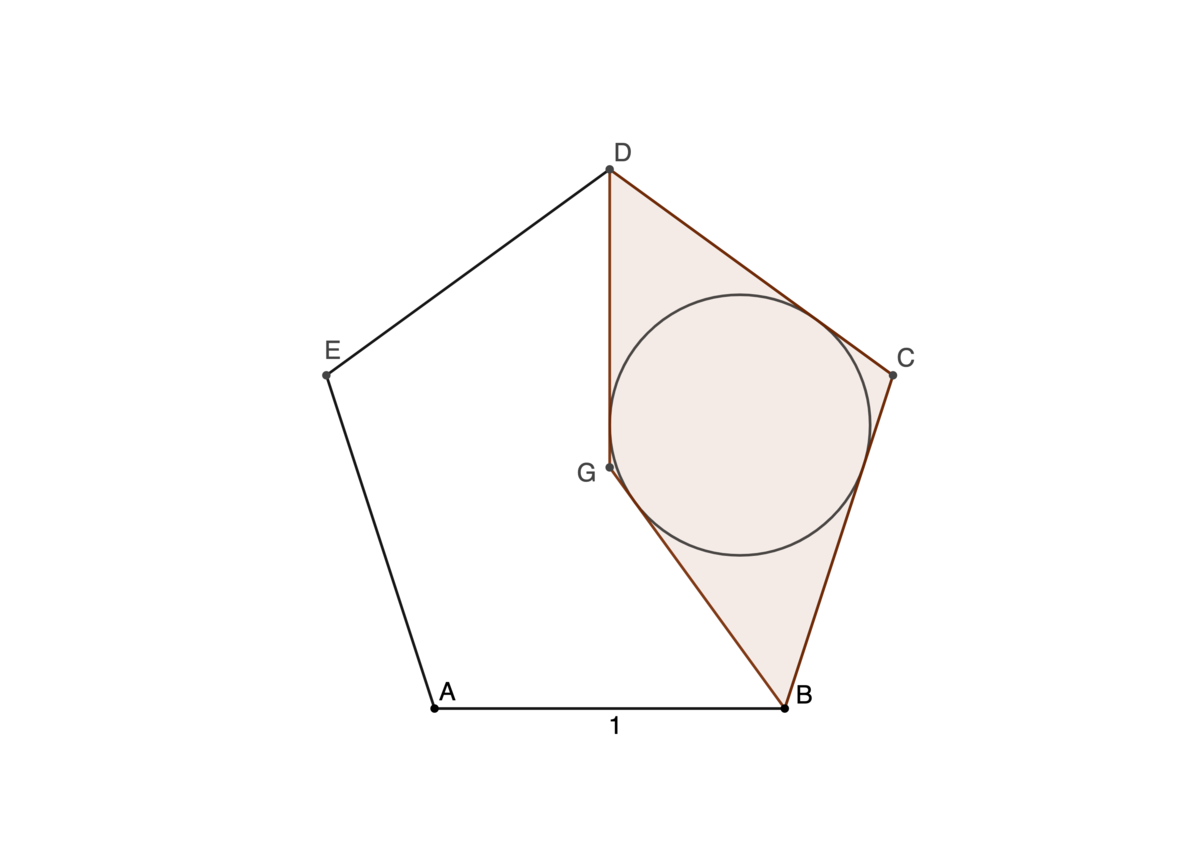
The centroid, G , of a regular pentagon, A B C D E with side length 1, is used to draw a tangential quadrilateral, G B C D . If the radius of its incircle is a root of f ( x ) = a x 4 + b x 3 + c x 2 + d x + e , where a > 0 , and g cd ( a , b , c , d , e ) = 1 , find f ( 1 ) .
The answer is 41.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
It's a common fact that sin ( 5 4 ∘ ) = 2 ϕ = 2 1 + 5 .
Apply double angle formula cos ( 2 X ) = 1 − 2 sin 2 ( X ) and triple angle formula cos ( 3 X ) = − 4 sin 3 ( X ) + 3 sin ( X ) , r = sin ( 8 1 ∘ ) sin ( 2 7 ∘ ) sin ( 5 4 ∘ ) = − 4 sin 3 ( 2 7 ∘ ) + 3 sin ( 2 7 ∘ ) sin ( 2 7 ∘ ) sin ( 5 4 ∘ ) = − 4 sin 2 ( 2 7 ∘ ) + 3 sin ( 5 4 ∘ ) = 1 + 2 cos ( 5 4 ∘ ) sin ( 5 4 ∘ ) = ⋯
The incentre I of the quadrilateral will lie on its angle bisectors, just as it does for a triangle. By symmetry, the angle bisector of ∠ B G D is just the line G D . To find I , and the inradius r , we can focus on triangle Δ G D C :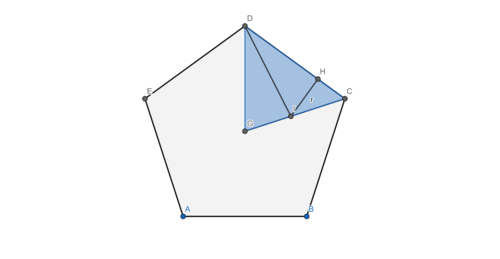
From known angles in the pentagon, ∠ C G D = 7 2 ∘ , ∠ G C D = ∠ G D C = 5 4 ∘ .
In triangle Δ I C D , then, ∠ I D C = 2 7 ∘ , ∠ D C I = 5 4 ∘ , ∠ C I D = 9 9 ∘ and C D = 1 (given).
The inradius r is just the length of the altitude I H ; we can find this by computing the area of Δ I C D . Using a formula for the area in terms of the angles and one side, this is [ I C D ] = 2 sin ∠ C I D C D 2 sin ∠ I C D ⋅ sin ∠ I D C = 2 sin 9 9 ∘ sin 2 7 ∘ ⋅ sin 5 4 ∘
We then have r = C D 2 [ I C D ] which works out to be r = 4 1 ( − 2 ( 2 + 5 ) + 5 0 + 2 2 5 )
This has minimal polynomial f ( x ) = 1 6 x 4 + 6 4 x 3 − 4 4 x 2 + 4 x + 1
and f ( 1 ) = 4 1 .
I had to use a lot of trig simplification here - basically bashing away at Wolfram|Alpha to get the algebraic form. An alternative approach might be to couch this in terms of complex numbers, or coordinate geometry, and try to avoid trig as much as possible.