Quadrilateral Inscribed In Semicircle A
A quadrilateral is inscribed in a semicircle of diameter 1 0 5
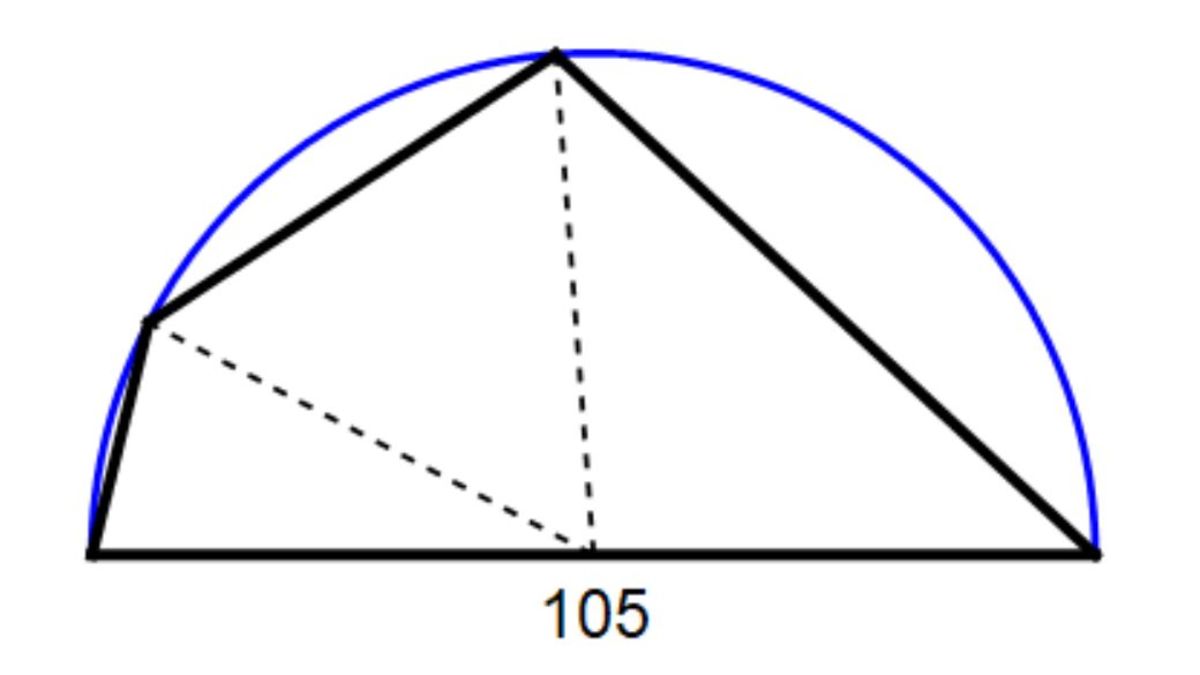
The three shorter sides are of integer lengths in arithmetic progression.
What's the length of the shortest side?
The answer is 25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Only one point. Though it is evident, you should mention that t is less than 1 0 5 in the step where you are showing that t ≤ 5 2 . :)
The above argument can be applied to show that for a general case of a diameter A D = d , if t is an integer between 5 d < t < 2 d such that t − x divides evenly into 4 d 3 and k 2 = 2 ( t − d ) ( t + d ) 2 ( 2 t − d ) is a square integer, then A B = t − k , B C = t , and C D = t + k are in an arithmetic progression.
The smallest diameter I could find (with the help of a computer program) that also fits the question's arithmetic progression criteria is A D = 3 0 , where A B = 3 , B C = 1 4 , and C D = 2 5 .
Since there is no other solution provided, I submit my numerical solution.
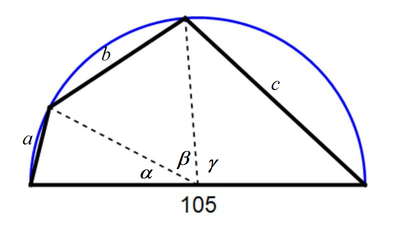
Let the three shorter side lengths of increasing length be a , b , and c and the angles they extend at the center of the semicircle be α , β , and γ respectively. Then we have a = 1 0 5 sin 2 α , b = 1 0 5 sin 2 β , and c = 1 0 5 sin 2 γ . Since 2 α + 2 β + 2 γ = 9 0 ∘ , we have:
b = 1 0 5 sin 2 β = 1 0 5 sin ( 9 0 ∘ − 2 α − 2 γ ) = 1 0 5 cos ( 2 α + 2 γ ) = 1 0 5 cos ( sin − 1 1 0 5 a + sin − 1 1 0 5 c )
We can find b from a and c . We just have to cast a large enough integral net of a and c to get the integral b . I used the following Microsoft spreadsheet for the net.
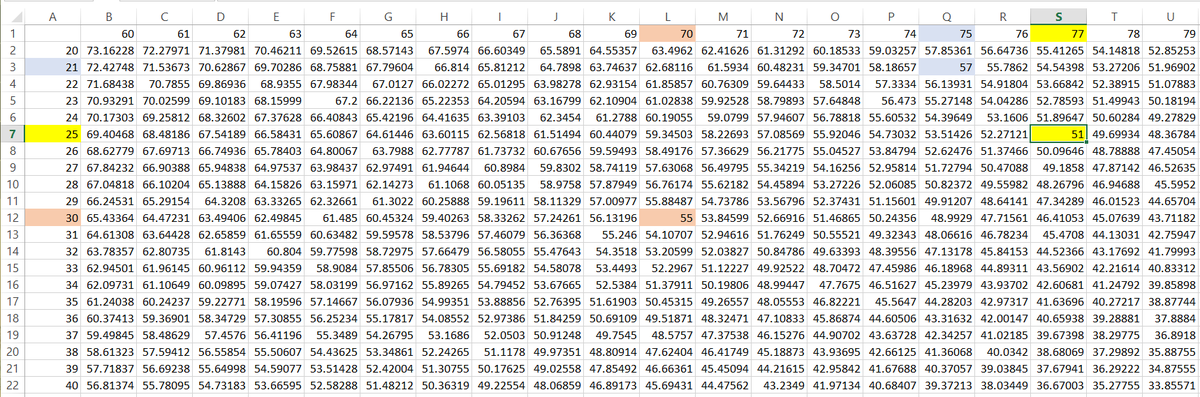
From the spreadsheet there are three integral solutions
⎩ ⎪ ⎨ ⎪ ⎧ a = 2 1 a = 2 5 a = 3 0 b = 5 7 b = 5 1 b = 5 5 c = 7 5 c = 7 7 c = 7 0 ⟹ a + c = 2 b ⟹ a + c = 2 b ⟹ a + c = 2 b rejected accepted rejected
Therefore the length of the shortest side is 2 5 .
I did the same way, and got a relation between a and c as
a = 4 c + 5 2 5 2 c 4 − 4 2 0 c 3 − 6 6 1 5 0 c 2 + 4 6 3 0 5 0 0 c + 6 0 7 7 5 3 1 2 5 − c ( 2 c + 1 0 5 ) and left after that.
Finding an integral value of c to yield an integral value of a can be done numerically. That's why I left the problem there.
Part of your expression can be factorized, so that
a = 4 c + 5 2 5 2 ( 1 0 5 + c ) ( 5 2 5 − c ) ( 1 0 5 − c ) − c ( 2 c + 1 0 5 )
so there's very few c to try out, once we have your relation. Similar relations can be found from the following which is true for cyclic quadrilaterals inscribed in a semicircle:
d 3 − ( a 2 + b 2 + c 2 ) d − 2 a b c = 0
where d is the longest side, or diameter. For example:
c = d 1 ( − a b + ( d + a ) ( d − a ) ( d + b ) ( d − b ) )
so that, again, because 1 0 5 = 3 × 5 × 7 , there's not much to try out.
Log in to reply
Even simpler:
From your expression of a , a necessary condition is for the radical part to be a perfect square, ( 5 2 5 − c ) ( 1 0 5 − c ) = d 2 for some integer d > 0 . This is essentially a Pell's equation .
With a constraint of c < 1 0 5 , there are only 4 solutions, namely, c = 2 5 , 4 1 , 7 7 , 9 3 . Trial and error shows that c = 7 7 is the only solution.
Log in to reply
You are good. I still don't know Pell much.
Great! I should have better tried to factorize the discriminant. Thanks for pointing this out.
The sides are ( 2 5 , 5 1 , 7 7 , 1 0 5 )
Well, sorry Professor Mendrin but i have to say i could not solve this without wolphram alpha after using Ptolemy (as David Vreken did) + sum of opposite angle doing 180° (as Mister Cheong did), the system of equation is too complicated.
Use WolframAlpha
Diophantine asin(x/105)+asin((x+y)/105)+asin((x+2y)/105)=pi/2,
or Ptolemy’s theorem
Diophantine (105^2-x^2)[105^2-(x+2y)^2]=[x(x+2y)+105(x+y)]^2
Gives, x=25 and y=26.
Label the vertices A , B , C , and D so that A D = 1 0 5 and A B < B C < C D < A D , and draw diagonals A C and B D . Since A B , B C , and C D are of integer lengths in an arithmetic progression, let A B = t − k , B C = t , and C D = t + k , where t and k are positive integers. Also, since B C < A D , that means t < 1 0 5 .
By Thales's Theorem, △ A B D is a right triangle, and by Pythagorean's Theorem B D = 1 0 5 2 − ( t − k ) 2 . Similarly, A C = 1 0 5 2 − ( t + k ) 2 .
By Ptolemy's Theorem, A C ⋅ B D = A B ⋅ C D + B C ⋅ A D , which after substitution becomes 1 0 5 2 − ( t − k ) 2 ⋅ 1 0 5 2 − ( t + k ) 2 = ( t − k ) ( t + k ) + 1 0 5 t and simplifies to 2 k 2 = t − 1 0 5 2 t 3 + 3 1 5 t 2 − 1 1 5 7 6 2 5 = t − 1 0 5 ( t + 1 0 5 ) 2 ( 2 t − 1 0 5 ) = 2 t 2 + 5 2 5 t + 5 5 1 2 5 + t − 1 0 5 4 6 3 0 5 0 0 .
Since A B = t − k > 0 , that means t > k and 2 t 2 > 2 k 2 . Therefore, 2 t 2 > 2 t 2 + 5 2 5 t + 5 5 1 2 5 + t − 1 0 5 4 6 3 0 5 0 0 , and since t < 1 0 5 , this solves to t > 2 2 0 5 ≥ 4 7 .
Since 2 k 2 > 0 , t − 1 0 5 ( t + 1 0 5 ) 2 ( 2 t − 1 0 5 ) > 0 , and since t < 1 0 5 , this means that t < 2 1 0 5 ≤ 5 2 .
Since 2 k 2 is an integer and 2 k 2 = 2 t 2 + 5 2 5 t + 5 5 1 2 5 + t − 1 0 5 4 6 3 0 5 0 0 , t − 1 0 5 must divide evenly into 4 6 3 0 5 0 0 = 2 2 3 3 5 3 7 3 . Out of the integers in the range 4 7 ≤ t ≤ 5 2 , only t = 5 1 gives a t − 1 0 5 value that divides evenly into 4 6 3 0 5 0 0 .
Therefore, t = 5 1 , k = 2 ( t − 1 0 5 ) ( t + 1 0 5 ) 2 ( 2 t − 1 0 5 ) = 2 ( 5 1 − 1 0 5 ) ( 5 1 + 1 0 5 ) 2 ( 2 ⋅ 5 1 − 1 0 5 ) = 2 6 , and A B = t − k = 5 1 − 2 6 = 2 5 .