Quadrilateral inside a quadrilateral
A B C D is a convex quadrilateral such that :
A D A E = A B B F = B C G C = C D H D = 3 1
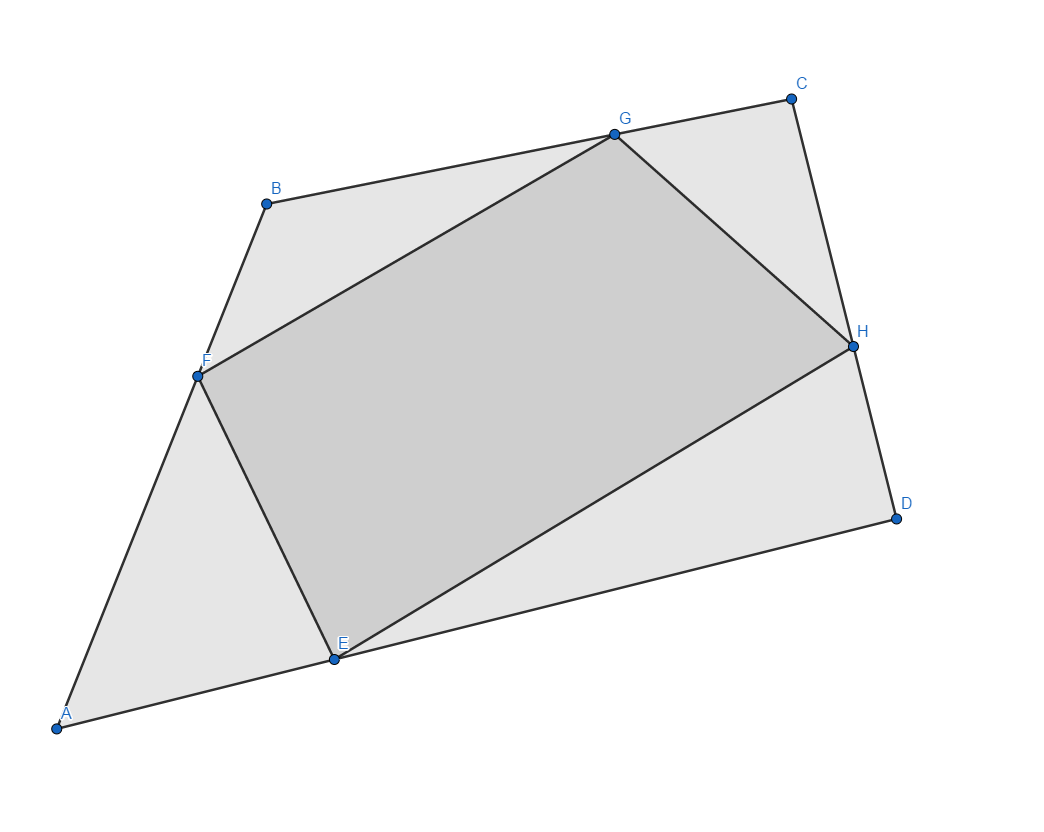
If A B C D area is equal to 1 and E F G H area is equal to b a with co-prime a , b find a + b
The answer is 14.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Let be a square of side lenght 1 and area 1. According to the statement, we can draw a new square which has the same length as the hypothenuse of the right triangle of side lenght 1/3 and 2/3.
Thus, this length measures: sqrt ((1/3) ^ 2 + (2/3) ^ 2).
Now, by calculating the area of this new square, we find 5/9. Plus 5 + 9 = 14.
The area of the outside quadrilateral is 2 1 × A B × A D × sin A + 2 1 × C B × C D × sin C = 2 1 × B A × B C × sin B + 2 1 × D A × D C × sin D = 1 △ A E F = 2 1 × A E × A F × sin A = 2 1 × 3 1 × A D × 3 2 × A B = 9 2 × 2 1 × A D × A B △ C G H = 2 1 × C G × C H × sin C = 9 2 × 2 1 × C B × C D × sin C △ A E F + △ C G H = 9 2 × ( 2 1 × A B × A D × sin A + 2 1 × C B × C D × sin C ) = 9 2 × 1 △ B F G + △ D E H = 9 2 So the inside quadrilateral is 1 − 9 2 − 9 2 = 9 5
Instead of finding directly E F G H area i'll find the triangle areas and subtract from A B C D
Consider the diagonal B D we know that A B D + B C D = 1 If you pay attention A B E have the same height as A B D but it's relative base is 3 A D so its area is equal to 3 A B D Now, look at A E F and A E B :
A E F has the same height as A E B but it's base is equal to 2 × 3 A B ∴
A E F area is equal to A E B × 3 2 that is equal to A B D × 9 2 )
If you do the same with triangle B C D you will get the same pattern. The sum of the "opposite" triangles it's equal to A B D × 9 2 + B C D × 9 2 = 9 2 ( A B D + B C D ) = 9 2 ( 1 ) Skipping unecessary calculations we get that A F E + B F G + C G H + D H E = 9 4 so E F G H = 1 − 9 4 = 9 5
Let a r e a ( Δ A C D ) = A , a r e a ( Δ A C B ) = B , a r e a ( Δ A B D ) = C , a r e a ( Δ B C D ) = D
Now, a r e a ( Δ A C D ) a r e a ( Δ E C D ) = A D E D = 3 2 ⟹ a r e a ( Δ E C D ) = 3 2 a r e a ( Δ A C D ) = 3 2 A
Also, a r e a ( Δ E C D ) a r e a ( Δ E H D ) = D C D H = 3 1 ⟹ a r e a ( Δ E H D ) = 3 1 a r e a ( Δ E C D ) = 3 1 ⋅ 3 2 A = 9 2 A ⋯ E q . 1
In the similar manner, a r e a ( Δ B F G ) = 9 2 B ⋯ E q . 2 a r e a ( Δ A E F ) = 9 2 C ⋯ E q . 3 a r e a ( Δ C G H ) = 9 2 D ⋯ E q . 4
Adding all these 4 equations we get,
a r e a ( Δ E H D ) + a r e a ( Δ B F G ) + a r e a ( Δ A E F ) + a r e a ( Δ C G H ) = 9 2 ( A + B ) + 9 2 ( C + D ) ⟹ a r e a ( A B C D ) − a r e a ( E F G H ) = 9 2 ⋅ 1 + 9 2 ⋅ 1 = 9 4 ⟹ a r e a ( E F G H ) = a r e a ( A B C D ) − 9 4 = 1 − 9 4 = 9 5
So, a = 5 , b = 9 ⟹ a + b = 1 4