Quadrilateral inside Triangle
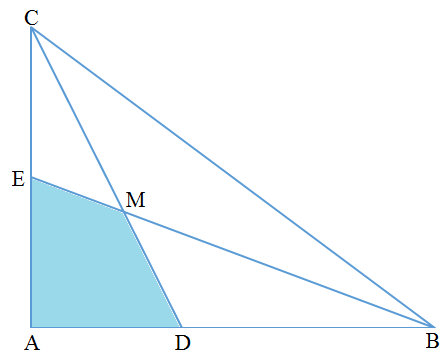
In △ A B C , ∠ A = 9 0 ∘ , A C = 3 and A B = 4 . C D is the angle bisector of ∠ A C B . Point E on A C is such that C E = A E . C D and B E intersect at M . If the area of quadrilateral A D M E = b a , where a and b are positive coprime integers, find a + b .
The answer is 133.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
L a T e X bisector theorem gives A D = 8 3 ⋅ 4 = 1 2 1
B E : y = − 8 3 x + 1 2 1 and C D : y = − 2 x + 3 intersect at ( 1 3 1 2 , 1 3 1 5 )
Divide A D M E in two triangle and a square
Area = 2 1 ⋅ ( 1 2 1 − 1 3 1 5 ) ⋅ 1 3 1 2 + 1 3 1 2 ⋅ 1 3 1 5 + 2 1 ⋅ ( 1 2 1 − 1 3 1 2 ) ⋅ 1 3 1 5 = 5 2 8 1 so the answer is 8 1 + 5 2 = 1 3 3
In my solution, I had found the ratios
D
B
A
D
,
M
D
C
M
by using
Menelaus' theorem
then by using the fact that Cevians divide the sides in the ratio equal to the ratio of the corresponding areas on either sides of the cevian, we will get the areas of
Δ
C
B
E
and
Δ
M
B
D
. Then by subtracting this area from the total area of the triangle get the answer.
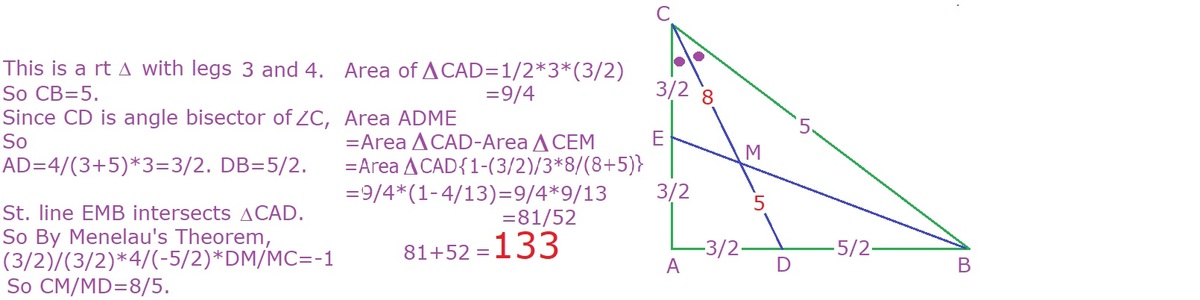
We know A C = 3 and A B = 4 , Therefore by Pythagorus theorem , B C = 5 and the area of right triangle A C B = 2 1 × 3 × 4 = 6 .
Also by Internal Angle Bisector Theorem ,
D B A D = C B A C
⇒ D B A D = 5 3
Now observe that in Δ C A D , E B divides the 3 sides of triangle in ratios E A C E , B D A B , M C B M
Therefore, by Menelaus's theorem
E A C E × B D A B × M C B M = 1 and we know E A C E = 1
Putting the known ratios,
1 1 × 5 8 × M C B M = 1 ⇒ M C B M = 8 5
So now area of
Δ M B D = D C M D × A B D B × Area of Δ A B C = 1 0 4 1 5 0
and the area of Δ C B E = 2 1 × Area of Δ A B C = 3 .
So the area of quadrilateral A E M D = 6 − 3 − 1 0 4 1 5 0 = 5 2 8 1
So the answer is 1 3 3
Place the triangle on a coordinate plane so that A is at ( 0 , 0 ) . Then B is at ( 4 , 0 ) , C is at ( 0 , 3 ) , and E is at ( 0 , 2 3 ) .
Since C D is the angle bisector of ∠ A C B with A C = 3 and A B = 4 , A D = 3 tan ( 2 1 tan − 1 ( 3 4 ) ) . Using the tangent half angle formula and Pythagorean's Theorem, A D = 3 ⋅ 5 4 1 − 5 3 = 2 3 . Therefore, D is at ( 2 3 , 0 ) .
Using the above coordinates, C D is on line y = − 2 x + 3 and E B is on line y = − 8 3 x + 2 3 . The intersection M is therefore at the solution to the two lines which is at ( 1 3 1 2 , 1 3 1 5 ) .
This means that △ A M D has a base of 2 3 and a height of 1 3 1 5 , and so an area of 2 1 2 3 1 3 1 5 = 5 2 4 5 ; and △ A M E has a base of 2 3 and a height of 1 3 1 2 , and so an area of 2 1 2 3 1 3 1 2 = 5 2 3 6 .
The area of quadrilateral A D M E is equal to the sum of the areas of △ A M D and △ A M E , which is 5 2 4 5 + 5 2 3 6 = 5 2 8 1 , and so a = 8 1 and b = 5 2 , and a + b = 1 3 3 .
Use coordinate Geometry, with A(0,0). And <ACD= ½ <ACB = ½ sin-1(4/5) = 26.625. So AD=3tan 26.625 = 3/2.We have D(3/2,0), E(0,3/2). The eqs. ofline CD : y = -2x + 3, and BE: y=(-3/8) x +3/2. The intersection point M(12/13, 15/13). The area of quadrilateral ADME= the area of ΔADM + the area of ΔADM + ΔAEM = ½ (3/2 . 15/13 + 3/2 . 12/13 ) = 81/52. So a+b=133
By the bisector theorem in △ C E B and pythagorean theorem (to find E B )
We get that E M = 2 6 3 7 3 and M B = 1 3 5 7 3
Again with bisector theorem but in △ A B C we get that A D = 2 3 and D B = 2 5
Now, by triangle similiarity △ A B E ~ △ D H B with this we can find D H and then calculate △ D M B area (we know M B ) in order to subtract from △ A B E .
Doing the boring calculation we get 3 − 5 2 7 5 = 5 2 8 1 then answer is 1 3 3