Quadrilateral Midpoint Areas

Note: this is an incomplete proof, for I have yet to figure out how to apply this to concave quadrilaterals.

---

Let us have quadrilateral $ABCD$ with the new "midpoint quadrilateral" $WXYZ$ :

Now, analyze the four triangles and their side lengths. Since $W$ is the midpoint of $AB$ , that means $AW\cong BW$ . Note that we can apply this to all of the sides. Knowing this, we can the reflect each triangle over its "midpoint side" ( $\triangle AWZ~\text{over}~WZ$ , etc.):

Since the sides don't overlap due to their congruence, this is a valid transformation. This will put all of the triangles on top of $WXYZ$ , which means the areas are the same. Since the areas are the same, $2\cdot A_{WXYZ} = A_{ABCD}$ $A_{WXYZ}=\boxed{\frac{1}{2}}\cdot A_{ABCD}$

Let $ABCD$ be a quadrilateral, and $EFGH$ be the new quadrilateral that is formed by joining the midpoints of adjacent sides.

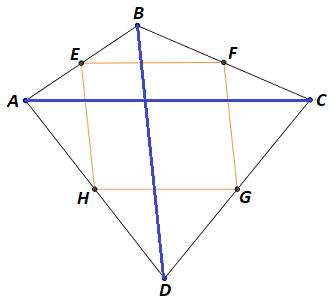
Then each side of $EFGH$ is a midsegment of a triangle whose base is one of the diagonals of $ABCD$ and whose sides are two of the sides of $ABCD$ . By the triangle midsegment theorem, $EF || AC$ and $GH || AC$ , so $EF || GH$ . Similarly, $FG || BD$ and $EH || BD$ , so $FG || EH$ . Therefore, $EFGH$ must be a parallelogram.

Now let $BK$ be the altitude of $\triangle ABC$ and $J$ the intersection of $BK$ and $EF$ (for concave quadrilaterals, let $A$ be the concave angle, and extend $EF$ for the intersection point $J$ ). Similarly, let $DL$ be the altitude of $\triangle ACD$ and $M$ the intersection of $DL$ and $GH$ . Let $p = EF$ , $q = JK$ , and $r = LM$ .

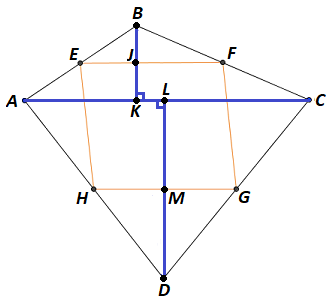
Once again by the triangle midsegment theorem, $EF = \frac{1}{2}AC$ , and since $p = EF$ , $AC = 2p$ . Since $\triangle BEF \sim \triangle BAC$ and corresponding sides $EF$ and $AC$ have a $\frac{1}{2}$ ratio, the heights $BJ$ and $BK$ also have a $\frac{1}{2}$ ratio, and since $q = JK$ , $BK = 2q$ . Similarly, since $r = LM$ , $DL = 2r$ .

The area $A_{ABCD}$ of quadrilateral $ABCD$ is equivalent to the combined areas of $\triangle ABC$ and $\triangle ADC$ , which are $\frac{1}{2} \cdot 2p \cdot 2q = 2pq$ and $\frac{1}{2} \cdot 2p \cdot 2r = 2pr$ respectively, so $A_{ABCD} = 2pq + 2pr = 2(pq + pr)$ . The area $A_{EFGH}$ of parallelogram $EFGH$ is $A_{EFGH} = p(q + r) = pq + pr$ . Therefore, $A_{EFGH} = \frac{1}{2}A_{ABCD}$ .

The above argument can be made for any quadrilateral $ABCD$ , whether it be a square, rectangle, concave, or convex. Therefore, if the midpoints of adjacent sides of any quadrilateral are joined, a parallelogram is always formed that is always half of the area of the original quadrilateral.