This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
good combination of theorems
how is my solution??
Alternative Proof:
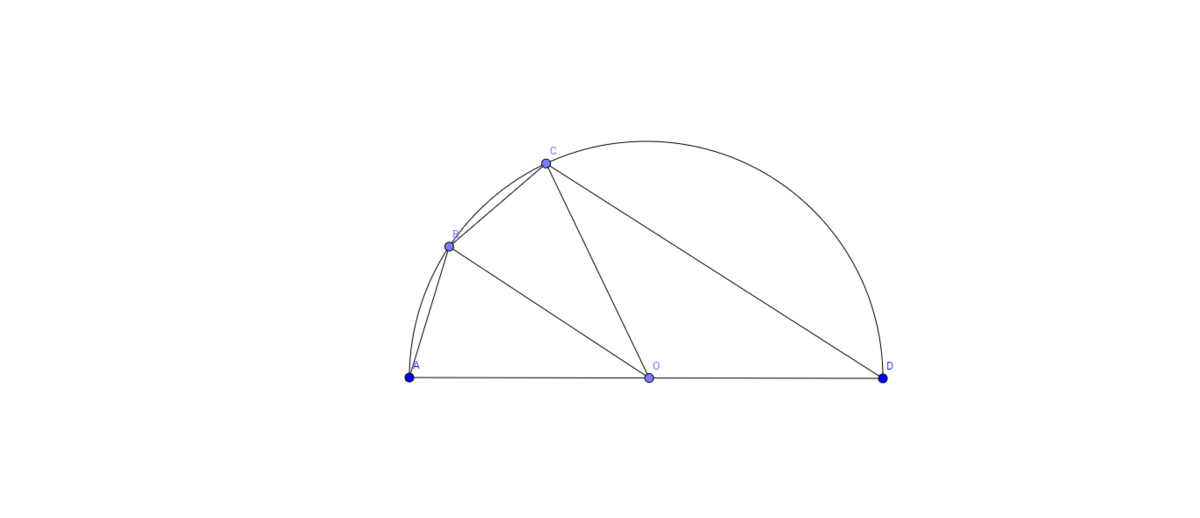
Let
∠
A
O
B
=
θ
.
Therefore
∠
C
O
D
=
π
−
2
θ
⇒
C
D
=
4
s
i
n
(
2
π
−
2
θ
)
=
4
c
o
s
θ
=
4
.
2
.
O
A
.
O
B
(
O
A
2
+
O
B
2
−
A
B
2
)
=
2
7
=
3
.
5
.
Good solution +1
Join B D and A C . ∠ A B D = 9 0 ∘ , ∠ A C D = 9 0 ∘ (Angle subtended at the semicircle)
Now by pythagorean theorem , we get B D = 4 2 − 1 2 = 1 5 and A C = 4 2 − C D 2 = 1 6 − C D 2 .
Now by ptolemy's theorem , A B ⋅ C D + B C ⋅ A D = A C ⋅ B D . or 1 ⋅ C D + 1 ⋅ 4 = 1 6 − C D 2 ⋅ 1 5 = 2 4 0 − 1 5 C D 2 .
Let C D = x . We have x + 4 = 2 4 0 − 1 5 x 2 or x 2 + 8 x + 1 6 = 2 4 0 − 1 5 x 2 or 1 6 x 2 + 8 x − 2 2 4 = 0 or 2 x 2 + x − 2 8 = 0 .
By quadratic formula we have x = 4 − 1 ± 1 2 − 4 × 2 × ( − 2 8 ) = 4 − 1 ± 1 5 = 4 1 4 = 3 . 5 (we have to consider only positive value as length of side cannot be negative).
Hence x = C D = 3 . 5 .