Quadrilaterals in a Triangle

Here are the $36$ quadrilaterals:

From the $3 \times 2$ convex quadrilateral near the top there are $(3 + 2 + 1)(2 + 1) = 18$ convex quadrilaterals (top two rows), and each of those convex quadrilaterals are the intersection of two triangles that make up a concave quadrilateral (bottom two rows), for a total of $2 \cdot 18 = \boxed{36}$ quadrilaterals.

There are $18$ convex quadrilaterals, all coming from the $2 \times 3$ block at the top. Each of these is in a 1-1 correspondence with the concave quadrilaterals by extending the sides downward to meet at the bottom. $18 \cdot 2= \boxed{36}$

Convex quadrilaterals: This is as same as counting the amount of rectangles in a $2\times3$ grid, so it's $(1+2)(1+2+3)=18.$

Concave quadrilaterals: Choose a big triangle, and cut out a smaller triangle will become a concave quadrilaterals. Counting and get 18.

So,there are 18+18=36 quadrilaterals.

Firstly, observe that bottom line cannot be a side of a quadrilateral, but only of triangles. Next, let's denote the group of lines (directions) which intersect with each other in left-bottom corner with A (there are 3 such lines) and the group of lines which intersect with each other at bottom-right corner with B (there are 4 such lines). Then, consider what happens when we choose four lines at random. If these four lines consists of two pairs of lines where one pair consists of lines that belong to group A and the other of those that belong to B, then we have defined two quadrilaterals, one convex and the other concave (look at the picture). On the other hand, if three or all four chosen lines are the lines belonging to single group, so either A or B, then we haven't defined any quadrilateral. 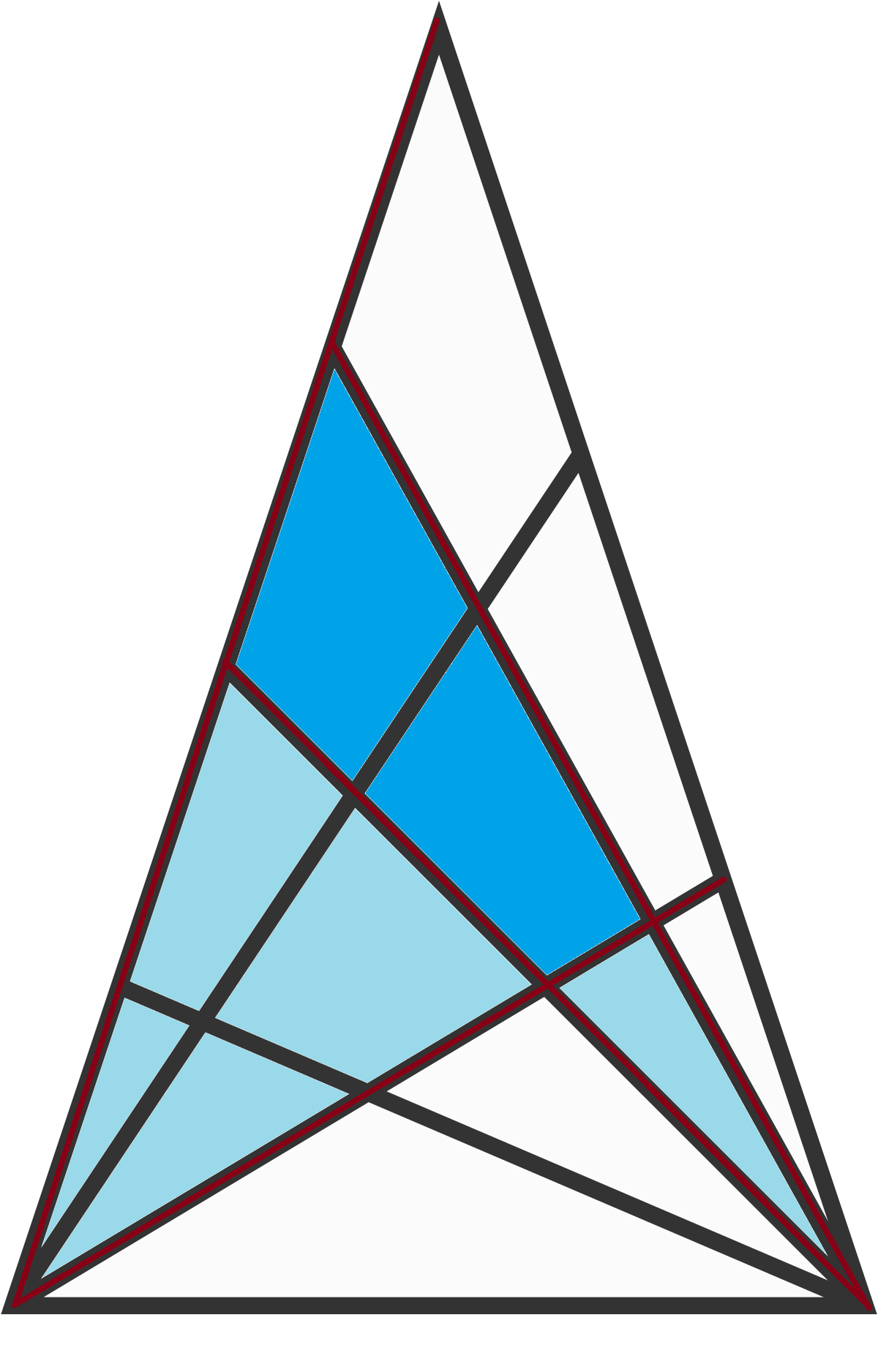Convex quadrilateral defined by given lines is colored in blue, while extension to concave quadrilateral is colored in light blue

Thus, we can calculate the number of quadrilaterals without explicitly counting them: $N = 2\times \binom{3}{2}\times \binom{4}{2} = \boxed{36}$

There are 8 lines drawn to make the shapes, and each shape can be either concave or convex. This means that each line has two possible methods of relating to a quadrilateral shape, meaning it has two dimensions. Each line is a component of all possible shapes that could be made, and all lines are arranged in a triangular (3-dimensional) formation. We are looking for four-dimensional quadrilaterals that can be built out of these shapes.

The construction of the problem is an ascending numerical order (2, 3, 4) that we want to find the top of (quadrilaterals). So we do the inverse of the relationship, from the smallest available shape (the lines).

8! = 8+7+6+5+4+3+2+1 = 36

More importantly though, the last question was also about factorials.

The correct answer is 36.

1) First if all disorder all shapes without four corners.

2) Count the remaining shapes, in this case six shapes with four corners are left.

3) Now you take the number of all remaining shapes with 4 corners high 2 = 6^(2) This way you are going to find out all possible conditions.

6 ^ (2) = 36