Quadruple somersault
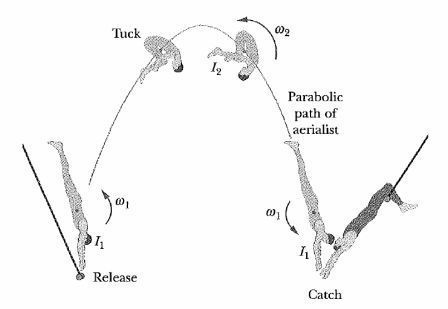 During a jump to his partner, an aerialist is to make a quadruple somersault lasting a
time
. For the first and last quarter-revolution, he is in the extended orientation shown in the figure, with rotational inertia
around his center of mass (the dot). During the rest of the flight he is in a tight tuck, with rotational inertia
What must be his angular speed
in
around his centre of mass during the tuck?
During a jump to his partner, an aerialist is to make a quadruple somersault lasting a
time
. For the first and last quarter-revolution, he is in the extended orientation shown in the figure, with rotational inertia
around his center of mass (the dot). During the rest of the flight he is in a tight tuck, with rotational inertia
What must be his angular speed
in
around his centre of mass during the tuck?
Liked it? try some more
The answer is 3.23.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
S i n c e t h e o n l y f o r c e a c t i n g o n h i m ( g r a v i t a i o n a l ) i s a c t i n g o n t h e C . O . M , a n g u l a r m o m e n t u m i s c o n s e r v e d 1 . I 1 ω 1 = I 2 ω 2 L e t t h e t i m e t a k e n t o p e r f o r m t h e f i r s t q u a t e r + l a s t q u a r t e r = t 1 N u m b e r o f r e v o l u t i o n s i n t 1 = 2 1 L e t t h e t i m e t a k e n t o p e r f o r m t h e r e s t o f t h e j u m p = t 2 N u m b e r o f r e v o l u t i o n s i n t 2 = 2 7 2 . 2 1 r e v = I 1 I 2 ω 2 × t 1 ( ω 1 = I 1 I 2 ω 2 f r o m a n g u l a r m o m e n t u m c o n s e r v a t i o n ) 3 . 2 7 r e v = ω 2 × t 2 D i v i d i n g t h e a b o v e t w o e q u a t i o n s , w e g e t 4 . t 2 − I 1 7 I 2 t 1 = 0 G i v e n : 5 . t 1 + t 2 = 1 . 8 7 S o l v i n g t h e a b o v e t w o l i n e a r e q u a t i o n s , w e g e t t 1 = 0 . 7 8 5 s t 2 = 1 . 0 8 5 s I n s e r t i n g t h e a b o v e v a l u e s i n e q 3 , w e g e t ω 2 = 3 . 2 3 r e v s − 1