Quantum Computing 1.1 -- Qubit measurement
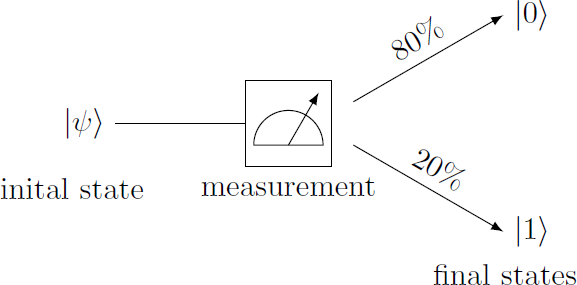
A quantum computer outputs a single qubit whose state is unknown. This qubit is measured so that the result is one of the two basis states and . This operation is performed many times, so that the relative frequencies for the results and are obtained. The state emerges with a probability of , while only of the cases yield the result .
What is a possible vector representation for the state ?
Note: The vectors are represented in the basis and are not normalized.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The absolute squares ∣ α ∣ 2 and ∣ β ∣ 2 of the vector components of the state ( α , β ) must be proportional to the probabilities 8 0 % and 2 0 % . Their ratio then results ∣ β ∣ 2 ∣ α ∣ 2 = 2 0 % 8 0 % = 4 We calculate this ratio for all vectors: ( 2 − 2 i 1 + i ) ( 4 − 1 ) ( 2 1 + i ) ( − i 2 ) ∣ 1 + i ∣ 2 ∣ 2 − 2 i ∣ 2 ∣ − 1 ∣ 2 ∣ 4 ∣ 2 ∣ 1 + i ∣ 2 ∣ 2 ∣ 2 2 2 ∣ − i ∣ 2 = ( 1 + i ) ( 1 − i ) ( 2 − 2 i ) ( 2 + 2 i ) = 1 2 + 1 2 2 2 + 2 2 = 4 = 1 6 = ( 1 + i ) ( 1 − i ) 4 = 1 2 + 1 2 4 = 2 = 4 ( − i ) ⋅ i = 4 1 Thus, only the vector ( 2 − 2 i , 1 + i ) corresponds to the measured probabilities.