Quantum Computing 1.2 -- Basis change
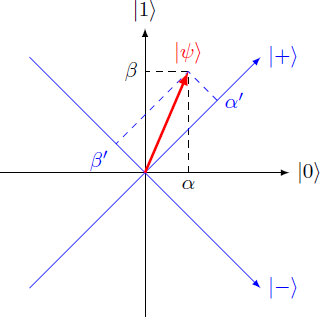
Instead of the usual basis vectors { ∣ 0 ⟩ , ∣ 1 ⟩ } for the qubit you can also use another pair of basis vectors: ∣ + ⟩ ∣ − ⟩ = 2 1 ( ∣ 0 ⟩ + ∣ 1 ⟩ ) = 2 1 ( ∣ 0 ⟩ − ∣ 1 ⟩ ) A qubit is in the state ∣ ψ ⟩ = 5 2 ∣ 0 ⟩ + 5 1 ∣ 1 ⟩ Determine the representation of the qubit in the new basis { ∣ + ⟩ , ∣ − ⟩ } : ∣ ψ ⟩ = α ′ ∣ + ⟩ + β ′ ∣ − ⟩ What is the result for the ratio β ′ α ′ ?
The answer is 3.00000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Instead of using a customary quantum mechanics approach, I thought of the problem like removing the x y term in the equation for a conic section, where you can rotate the coordinate axis by a certain angle to make the conic "perpendicular" to the coordinate axis. Alternatively, you can think of the process as changing the basis vectors for a vector. Treating the state of the qubit as a vector, let the angle between the vector and the original positive horizontal axis to be θ and the angle the axis are rotated by ϕ . The vector v ^ = ⟨ x ′ , y ′ ⟩ , which coordinates correspond to the vector ⟨ x , y ⟩ on the rotated axis, can be found by the following equations:
x ′ = ∥ v ^ ∥ cos ( ϕ − θ ) y ′ = ∥ v ^ ∥ sin ( ϕ − θ )
Since ∣ ψ ⟩ = ⟨ 5 2 , 5 1 ⟩ as a vector, θ = arctan ( 2 1 ) , and ∥ ∣ ψ ⟩ ∥ = 5 4 + 5 1 = 1 . For our new axis ϕ = 4 π , so we can calculate that:
x ′ = ∥ ∣ ψ ⟩ ∥ cos ( ϕ − θ ) = cos ( 4 π − arctan ( 2 1 ) ) = cos ( 4 π ) cos ( arctan ( 2 1 ) ) + sin ( 4 π ) sin ( arctan ( 2 1 ) ) = 2 × 5 2 × 2 + 2 × 5 2 × 1 = 1 0 3 1 0 y ′ = ∥ ∣ ψ ⟩ ∥ sin ( ϕ − θ ) = sin ( 4 π − arctan ( 2 1 ) ) = sin ( 4 π ) cos ( arctan ( 2 1 ) ) − cos ( 4 π ) sin ( arctan ( 2 1 ) ) = 2 × 5 2 × 2 − 2 × 5 2 × 1 = 1 0 1 0
So in the rotated axis ∣ ψ ⟩ = ⟨ 1 0 3 1 0 , 1 0 1 0 ⟩ , and if we convert this back into a qubit,
∣ ψ ⟩ = 1 0 3 1 0 ∣ + ⟩ + 1 0 1 0 ∣ − ⟩
Therefore, β ′ α ′ = 3
Here I show a very formal calculation using the Dirac notation. Although this method seems unnecessarily complicated for this problem, it is usually the method of choice in quantum mechanics.
We first calculate all scalar products for the vectors ∣ + ⟩ and ∣ − ⟩ : ⟨ + ∣ + ⟩ ⟨ − ∣ − ⟩ ⟨ + ∣ − ⟩ ⟨ ± ∣ 0 ⟩ ⟨ ± ∣ 1 ⟩ = ( 2 1 ⟨ 0 ∣ + 2 1 ⟨ 1 ∣ ) ( 2 1 ∣ 0 ⟩ + 2 1 ∣ 1 ⟩ ) = 2 1 ( ⟨ 0 ∣ 0 ⟩ + ⟨ 0 ∣ 1 ⟩ + ⟨ 1 ∣ 0 ⟩ + ⟨ 1 ∣ 1 ⟩ ) = 2 1 ( 1 + 0 + 0 + 1 ) = 1 = ( 2 1 ⟨ 0 ∣ − 2 1 ⟨ 1 ∣ ) ( 2 1 ∣ 0 ⟩ − 2 1 ∣ 1 ⟩ ) = 2 1 ( ⟨ 0 ∣ 0 ⟩ − ⟨ 0 ∣ 1 ⟩ − ⟨ 1 ∣ 0 ⟩ + ⟨ 1 ∣ 1 ⟩ ) = 2 1 ( 1 − 0 − 0 + 1 ) = 1 = ( 2 1 ⟨ 0 ∣ + 2 1 ⟨ 1 ∣ ) ( 2 1 ∣ 0 ⟩ − 2 1 ∣ 1 ⟩ ) = 2 1 ( ⟨ 0 ∣ 0 ⟩ − ⟨ 0 ∣ 1 ⟩ + ⟨ 1 ∣ 0 ⟩ − ⟨ 1 ∣ 1 ⟩ ) = 2 1 ( 1 − 0 + 0 − 1 ) = 0 = ( 2 1 ⟨ 0 ∣ ± 2 1 ⟨ 1 ∣ ) ∣ 0 ⟩ = 2 1 ( ⟨ 0 ∣ 0 ⟩ ± ⟨ 1 ∣ 0 ⟩ ) = 2 1 ( 1 ± 0 ) = 2 1 = ( 2 1 ⟨ 0 ∣ ± 2 1 ⟨ 1 ∣ ) ∣ 1 ⟩ = 2 1 ( ⟨ 0 ∣ 1 ⟩ ± ⟨ 1 ∣ 1 ⟩ ) = 2 1 ( 0 ± 1 ) = ± 2 1 The vectors ∣ + ⟩ and ∣ − ⟩ are thus normalized and orthogonal to each other. Therefore we obtain a representation of the unit matrix by E = ∣ + ⟩ ⟨ + ∣ + ∣ − ⟩ ⟨ − ∣ . We multiply this unit matrix with the state vector: ∣ ψ ⟩ = ( ∣ + ⟩ ⟨ + ∣ + ∣ − ⟩ ⟨ − ∣ ) ∣ ψ ⟩ = ∣ + ⟩ ⟨ + ∣ ( 5 2 ∣ 0 ⟩ + 5 1 ∣ 1 ⟩ ) + ∣ − ⟩ ⟨ − ∣ ( 5 2 ∣ 0 ⟩ + 5 1 ∣ 1 ⟩ ) = ( 5 2 ⟨ + ∣ 0 ⟩ + 5 1 ⟨ + ∣ 1 ⟩ ) ∣ + ⟩ + ( 5 2 ⟨ − ∣ 0 ⟩ + 5 1 ⟨ − ∣ 1 ⟩ ) ∣ − ⟩ = ( 5 2 2 1 + 5 1 2 1 ) ∣ + ⟩ + ( 5 2 2 1 − 5 1 2 1 ) ∣ − ⟩ = 1 0 3 ∣ + ⟩ + 1 0 1 ∣ − ⟩ Thus, a ′ = 1 0 3 , b ′ = 1 0 1 ⇒ b ′ a ′ = 3