Quantum Computing 1.3 -- Polarizers

The probability that a $|0\rangle$ photon passes through a $30^\circ$ filter is $\cos^2 (30^\circ) = \frac{3}{4}$ . So, the probability the photon passes through three successive filters, each $30^\circ$ more than the last, is $\left( \frac{3}{4} \right)^3 = \frac{27}{64} \approx 42\%$ .

Minutephysics and 3Blue1Brown collaborated on a video about quantum polarization and Bell's theorem that not only details what you need to know for this problem but also talks about some interesting implications of the quantum polarization effect. I watched this video when it came out last year and it stuck with me well enough that I was able to do this problem so it's a good, clear video, well worth a look if you're interested.

One can represent the passage of a photon through the three polattering filters as a decision tree.

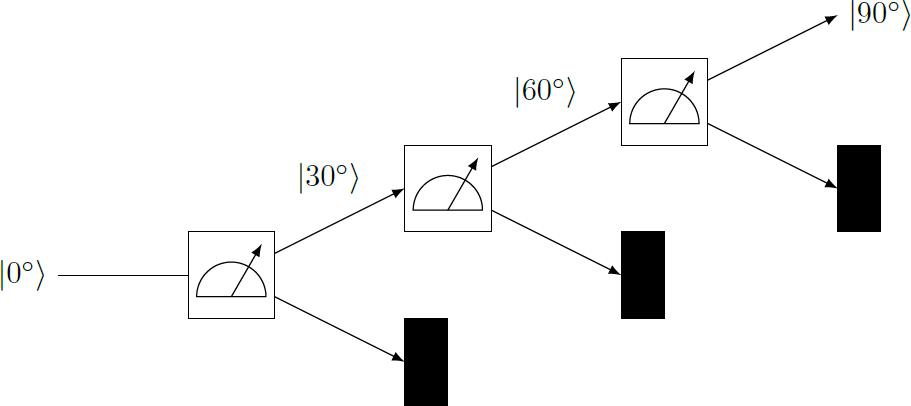
However, we start from the general case that we have $n$ polarization filters, each with the angle $\alpha_k = \frac {k} {n} \cdot 90 ^ \circ$ , $k = 1,2, \dots, n$ . The photon. that has already passed $k$ filters, has the polarization $| \alpha_k \rangle$ . This state can be represented by $\begin{aligned} |\alpha_k \rangle &= (|\alpha_{k+1} \rangle \langle \alpha_{k+1}| + |\alpha_{k+1} + 90^\circ \rangle \langle \alpha_{k+1} + 90^\circ|) |\alpha_k \rangle \\ &= \langle \alpha_{k+1}| \alpha_k \rangle |\alpha_{k+1} \rangle + \langle \alpha_{k+1} + 90^\circ| \alpha_k \rangle |\alpha_{k+1} + 90^\circ \rangle \end{aligned}$ The probability that the photon also passes the $k + 1$ filter is $\begin{aligned} |\langle \alpha_{k+1}| \alpha_k \rangle|^2 &= | (\cos \alpha_{k+1} \langle 0^\circ | + \sin \alpha_{k+1} \langle 90^\circ |) (\cos \alpha_{k} | 0^\circ \rangle + \sin \alpha_{k} | 90^\circ \rangle ) |^2 \\ &= |\cos \alpha_{k+1} \cos \alpha_{k} + \sin \alpha_{k+1} \sin \alpha_{k}|^2\\ &= |\cos(\alpha_{k+1} - \alpha_{k})|^2 \\ &= \left|\cos \frac{90^\circ}{n}\right|^2 \end{aligned}$ In particular, this probability is independent of $k$ . The total probability $P_n$ that the photon passes through all $n$ polarization filters therefore results from multiplying all individual probabilities: $P_n = \left|\cos \frac{90^\circ}{n}\right|^{2n}$ Thus, in the case $n= 3$ we get $P_3 = \left|\cos 30^\circ \right|^{6} = \left|\frac{\sqrt{3}}{2} \right|^{6} = \frac{3^3}{2^6} = \frac{27}{64} \approx 42 \,\%$ and the limiting case results to $\begin{aligned} \lim_{n\to\infty} P_n &= \lim_{n\to\infty} \left|\cos \frac{\pi}{2 n}\right|^{2n} \\ &= \lim_{n\to\infty} \exp \left(2n \cdot\log(\cos \frac{\pi}{2 n})\right) \\ &= \exp \left( \lim_{n\to\infty} \frac{\log(\cos \frac{\pi}{2 n})}{\frac{1}{2 n}}\right) & &|\text{apply L'Hospital rule}\\ &= \exp \left( \lim_{n\to\infty} \frac{-\frac{\pi}{2n^2}\frac{\sin \frac{\pi}{2 n}}{\cos \frac{\pi}{2 n}}}{-\frac{1}{2 n^2}}\right) \\ &= \exp \left( \lim_{n\to\infty} \pi \frac{\sin \frac{\pi}{2 n}}{\cos \frac{\pi}{2 n}}\right)\\ &= \exp(0) \\ &= 1 \end{aligned}$ This means that the photon is not absorbed, but passes through the polarizing filters in any case. Repeated lossless measurement changes the state of the photon from $| 0 ^ \circ \rangle$ to $| 90 ^ \circ \rangle$ . This is an example how measurements can alter a system to the complete opposite.

At each filter the 30° component's intensity reduces by square of it's amplitude which is (cos(30°))^2=(3/4). After three successive 30° filters it will reduce by (3/4)^3~0.42, and that is the answer to this problem.