Quantum Computing 1.4 -- Bloch sphere
 Every state
∣
ψ
⟩
of a qubit can be represented in the form
∣
ψ
⟩
=
e
i
γ
⋅
(
cos
2
θ
∣
0
⟩
+
e
i
ϕ
sin
2
θ
∣
1
⟩
)
,
θ
∈
[
0
,
π
]
,
ϕ
∈
[
0
,
2
π
]
The prefactor
e
i
γ
is without physical meaning.
The state is characterized by two angles
θ
and
ϕ
.
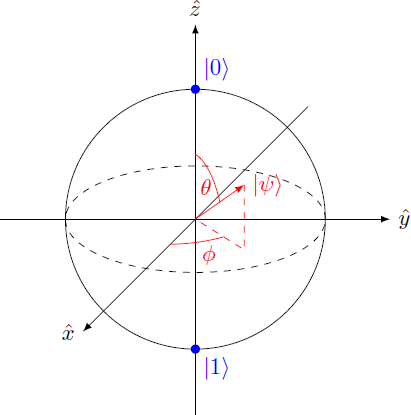
If you interpret these angles as latitude and longitude, they will set a point on a sphere's surface.
In this way we get a one-to-one mapping of the quantum state onto a unit sphere
∣
ψ
⟩
↦
r
=
⎝
⎛
cos
ϕ
sin
θ
sin
ϕ
sin
θ
cos
θ
⎠
⎞
∈
R
3
This representation of the qubit is called a Bloch sphere. In particular, the two basis states
∣
0
⟩
and
∣
1
⟩
map respectively to the north and south pole of the unit sphere.
Every state
∣
ψ
⟩
of a qubit can be represented in the form
∣
ψ
⟩
=
e
i
γ
⋅
(
cos
2
θ
∣
0
⟩
+
e
i
ϕ
sin
2
θ
∣
1
⟩
)
,
θ
∈
[
0
,
π
]
,
ϕ
∈
[
0
,
2
π
]
The prefactor
e
i
γ
is without physical meaning.
The state is characterized by two angles
θ
and
ϕ
.
If you interpret these angles as latitude and longitude, they will set a point on a sphere's surface.
In this way we get a one-to-one mapping of the quantum state onto a unit sphere
∣
ψ
⟩
↦
r
=
⎝
⎛
cos
ϕ
sin
θ
sin
ϕ
sin
θ
cos
θ
⎠
⎞
∈
R
3
This representation of the qubit is called a Bloch sphere. In particular, the two basis states
∣
0
⟩
and
∣
1
⟩
map respectively to the north and south pole of the unit sphere.
Given the point r = ⎝ ⎛ 3 / 8 3 / 8 1 / 2 ⎠ ⎞ on the Bloch sphere. What is the associated state of the qubit?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The angle θ can be derived from the z-coordinate of the vector. With the help of the cosine additon formula and the Pythagorean theorem, we get an expression for cos ( θ / 2 ) and sin ( θ / 2 ) : ⇒ z = cos θ cos 2 θ sin 2 θ = cos 2 2 θ − sin 2 2 θ = 2 cos 2 2 θ − 1 = 1 − 2 sin 2 2 θ = 2 1 + cos θ = 2 1 + z , = 2 1 − cos θ = 2 1 − z ∣ cosine addition formula ∣ Pythagoras cos 2 x + sin 2 x = 1 The phase angle ϕ is determined by the ratio between y- and x-coordinate: ⇒ ⇒ ⇒ x y cos ϕ sin ϕ e i ϕ = cos ϕ sin ϕ = cos ϕ 1 − cos 2 ϕ = cos 2 ϕ 1 − 1 = 1 + ( y / x ) 2 1 , = 1 − cos 2 ϕ = 1 + ( y / x ) 2 y / x = cos ϕ + i sin ϕ = 1 + ( y / x ) 2 1 + i y / x ∣ Pythagoras cos 2 x + sin 2 x = 1 The general solution for the state is accordingly ∣ ψ ⟩ = 2 1 + z ∣ 0 ⟩ + 2 1 − z 1 + ( y / x ) 2 1 + i y / x ∣ 1 ⟩ in our case is z = 1 / 2 and x = y = 3 / 8 , so that ∣ ψ ⟩ = 2 3 ∣ 0 ⟩ + 8 1 + i ∣ 1 ⟩