Quantum Computing 2.1 -- Composition of quantum gates

Computer Science Level 2

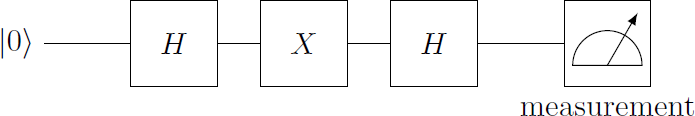
For a single qubit in the initial state ∣ 0 ⟩ | 0 \rangle , the quantum operations H H , X X , and H H are applied sequentially. At the end, the qubit is measured. What is the probability of getting the initial state ∣ 0 ⟩ | 0 \rangle back when measuring?

Details and assumptions: The basis states ∣ 0 ⟩ | 0 \rangle and ∣ 1 ⟩ | 1 \rangle of the qubit can be represented by two-dimensional unit vectors: ∣ 0 ⟩ = ( 1 0 ) , ∣ 1 ⟩ = ( 0 1 ) |0 \rangle = \left( \begin{array}{c} 1 \\ 0 \end{array} \right), \quad |1 \rangle = \left( \begin{array}{c} 0 \\ 1 \end{array} \right) In this basis, the quantum operations H H and X X can be represented as matrices: H = 1 2 ( 1 1 1 − 1 ) ( Hadamard-Gate ) X = ( 0 1 1 0 ) ( NOT-Gate ) \begin{aligned} H &= \frac{1}{\sqrt{2}} \left( \begin{array}{cc} 1 & 1 \\ 1 & - 1 \end{array}\right) & & (\text{Hadamard-Gate}) \\ X &= \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right) && (\text{NOT-Gate}) \end{aligned}

75 % 0 % 50 % 100 % 25 %

Markus Michelmann by Markus Michelmann , 35, Germany

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

The operator sequence H X H HXH is calculated by matrix multiplication H X H = 1 2 ( 1 1 1 − 1 ) ⋅ ( 0 1 1 0 ) ⋅ ( 1 1 1 − 1 ) = 1 2 ( 1 1 1 − 1 ) ⋅ ( 1 − 1 1 1 ) = 1 2 ( 2 0 0 − 2 ) = ( 1 0 0 − 1 ) = Z \begin{aligned} H X H &= \frac{1}{2} \left( \begin{array}{cc} 1 & 1 \\ 1 & - 1 \end{array}\right) \cdot \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right) \cdot \left( \begin{array}{cc} 1 & 1 \\ 1 & - 1 \end{array}\right) \\ &= \frac{1}{2} \left( \begin{array}{cc} 1 & 1 \\ 1 & - 1 \end{array}\right) \cdot \left( \begin{array}{cc} 1 & -1 \\ 1 & 1 \end{array}\right) \\ &= \frac{1}{2} \left( \begin{array}{cc} 2 & 0 \\ 0 & -2 \end{array}\right) \\ &= \left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right) = Z \end{aligned} The result is the quantum gate Z Z (phase shift). Applying this gate on the state ∣ 0 ⟩ |0\rangle results Z ∣ 0 ⟩ = ( 1 0 0 − 1 ) ( 1 0 ) = ( 1 0 ) = ∣ 0 ⟩ Z |0\rangle = \left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right) \left( \begin{array}{c} 1 \\ 0 \end{array}\right) = \left( \begin{array}{c} 1 \\ 0 \end{array}\right) = |0\rangle Therefore, the state is not changed at all.

2 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...