Quantum Computing 2.3 -- Hadamard gate on the Bloch sphere
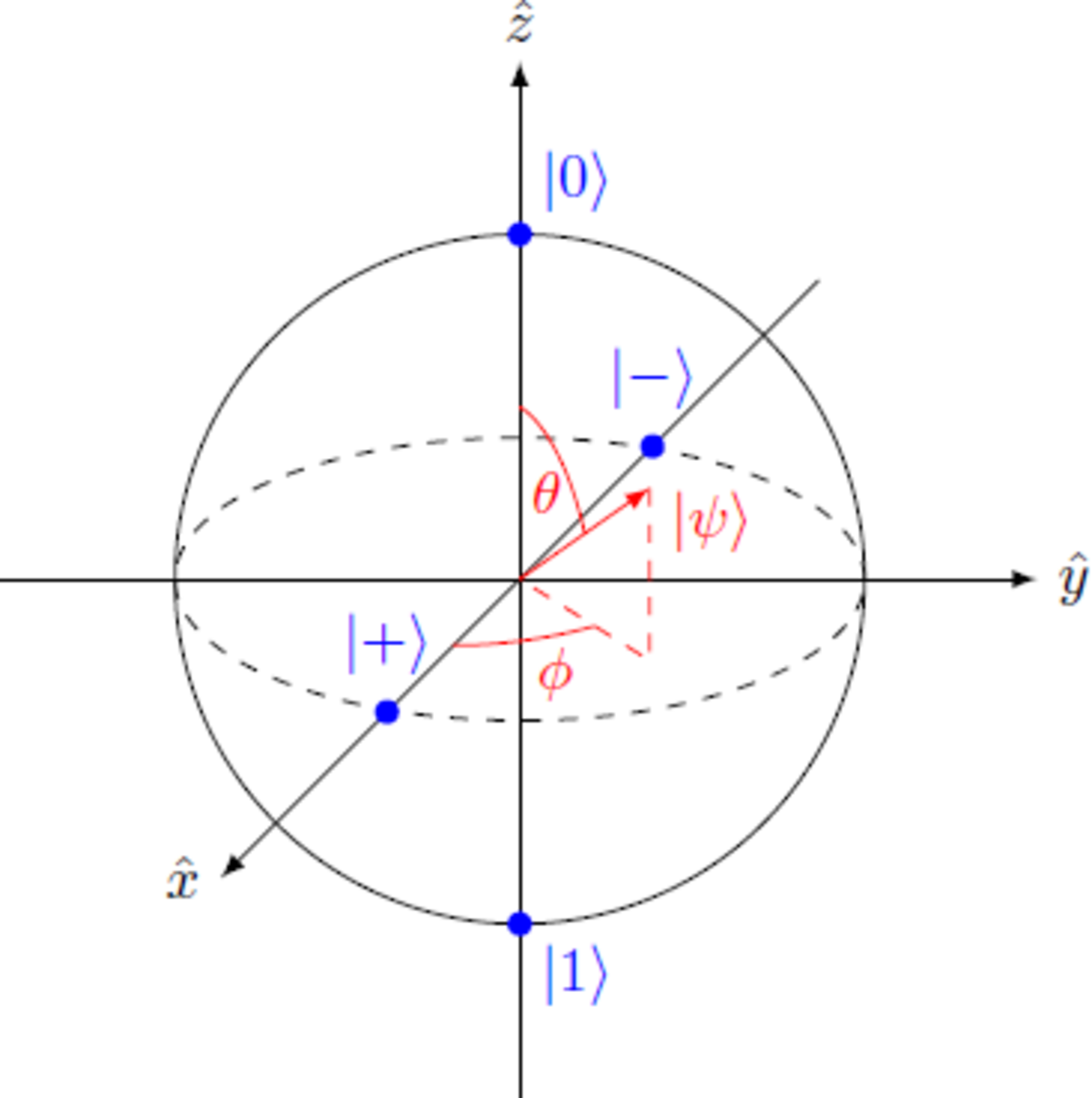
As we have already seen problem 1.4 , one can uniquely assign each state of a qubit to a point on a so-called Bloch sphere. The two-dimensional state vector is mapped to a vector in three-dimensional space For example, the two basis states and are each mapped north and south pole of the bloch sphere and the superposition states and became opposite points on the equator of the sphere.
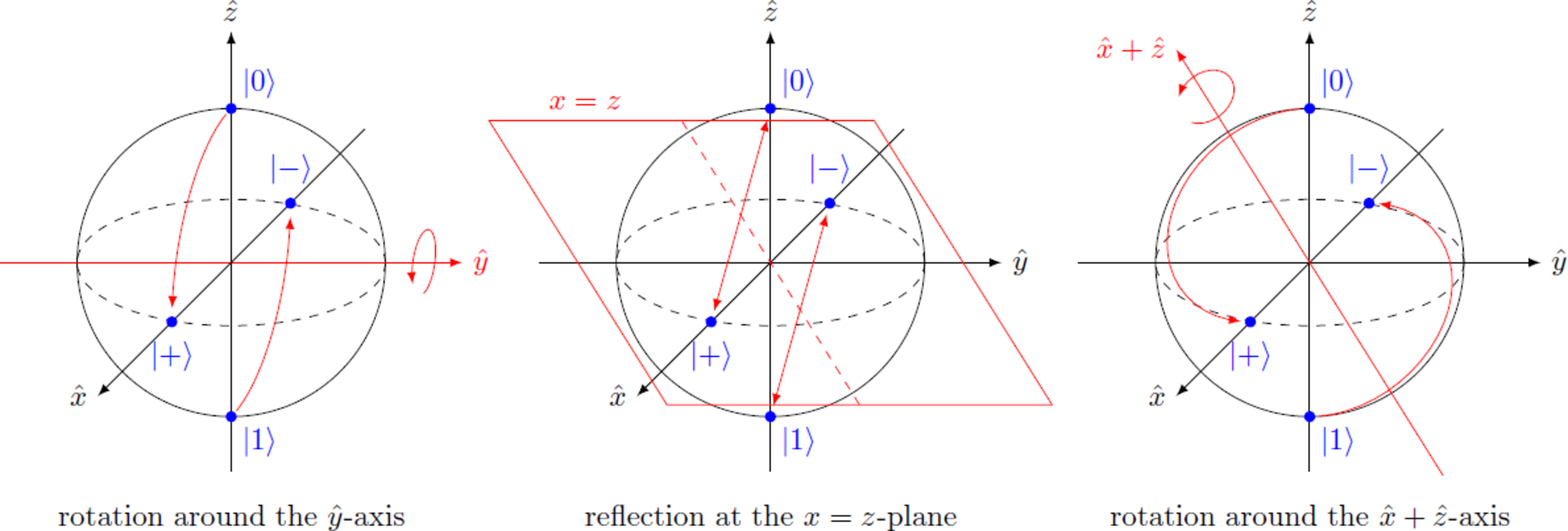
We now consider the Hadamard gate given in the -basis by the matrix Visualize the effect of the Hadamard gate in the Bloch sphere representation.
What is the geometric equivalent of the operator in three-dimensional space?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We first describe the geometric operations in three-dimensional space through matrices. The reflection at an origin plane with the normal vector n ^ = ( n x , n y , n z ) is generally described by the operation r R n ^ ↦ r − 2 ( r ⋅ n ^ ) n ^ = ( I − 2 n ^ ⊗ n ^ ) ⋅ r = : R n ^ ⋅ r = ⎝ ⎛ 1 − 2 n x 2 − 2 n x n y − 2 n x n z − 2 n x n y 1 − 2 n y 2 − 2 n y n z − 2 n x n z − 2 n y n z 1 − 2 n z 2 ⎠ ⎞ For the plane x = z we have n ^ = 2 1 ( − 1 , 0 , 1 ) and therefore R x = z = ⎝ ⎛ 0 0 1 0 1 0 1 0 0 ⎠ ⎞ A general rotation around the axis n ^ with the angle α can be written in three-dimensional space as r R n ^ ( α ) ↦ ( n ^ ⋅ r ) n ^ + cos α ( n ^ × r ) × n ^ + sin α ( n ^ × r ) = ( ( 1 − cos α ) n ^ ⊗ n ^ + I cos ( α ) + sin α i = x , y , z ∑ ( n ^ × i ^ ) ⊗ i ^ ) ⋅ r = : R n ^ ( α ) ⋅ r = ⎝ ⎛ n x 2 ( 1 − cos α ) + cos α n x n y ( 1 − cos α ) − n z sin α n x n z ( 1 − cos α ) − n y sin α n x n y ( 1 − cos α ) − n z sin α n y 2 ( 1 − cos α ) + cos α n x n y ( 1 − cos α ) + n z sin α n x n z ( 1 − cos α ) + n y sin α n y n z ( 1 − cos α ) − n x sin α n z 2 ( 1 − cos α ) + cos α ⎠ ⎞ in our case, the rotation axes are n ^ = ( 0 , 1 , 0 ) and n ^ = 2 1 ( 1 , 0 , 1 ) and the rotation angles are α = π / 2 and α = π . Thus, the rotation matrices yield R y ^ ( π / 2 ) R x ^ + z ^ ( π ) = ⎝ ⎛ 0 0 − 1 0 1 0 1 0 0 ⎠ ⎞ = ⎝ ⎛ 0 0 1 0 − 1 0 1 0 0 ⎠ ⎞ Obviously, these operations are different so you can try different example states to see which of these operations is the right one. You will find out that only the rotation around the x ^ + z ^ -axis always gives the correct results. We now want to prove that this rotation is indeed equivalent to the Hadamard operation.
Application of the Hadamard gate yields ⇒ ⇒ ⇒ ( α ′ β ′ ) α ′ β ′ = tan 2 θ ′ e i ϕ ′ tan ϕ ′ tan 2 θ ′ = 2 1 ( 1 1 1 − 1 ) ( cos 2 θ sin 2 θ e i ϕ ) = ( cos 2 θ + sin 2 θ e i ϕ cos 2 θ − sin 2 θ e i ϕ ) = e i γ ′ ( cos 2 θ ′ sin 2 θ ′ e i ϕ ′ ) = cos 2 θ + sin 2 θ e i ϕ cos 2 θ − sin 2 θ e i ϕ = cos 2 θ + sin 2 θ e i ϕ cos 2 θ − sin 2 θ e i ϕ cos 2 θ + sin 2 θ e − i ϕ cos 2 θ + sin 2 θ e − i ϕ = cos 2 2 θ + sin 2 2 θ + sin 2 θ cos 2 θ ( e i ϕ + e − i ϕ ) cos 2 2 θ − sin 2 2 θ − sin 2 θ cos 2 θ ( e i ϕ − e − i ϕ ) = 1 + sin θ cos ϕ cos θ − i sin θ sin ϕ = − cos θ sin θ sin ϕ = ∣ ∣ ∣ ∣ 1 + sin θ cos ϕ cos θ − i sin θ sin ϕ ∣ ∣ ∣ ∣ = 1 + sin θ cos ϕ cos 2 θ + sin 2 θ sin 2 ϕ = 1 + sin θ cos ϕ 1 − sin 2 θ cos 2 ϕ = 1 + sin θ cos ϕ 1 − sin θ cos ϕ The rotation around the x ^ + z ^ -axis yields ⇒ ⇒ ⎝ ⎛ x ′ y ′ z ′ ⎠ ⎞ = ⎝ ⎛ cos ϕ ′ sin θ ′ sin ϕ ′ sin θ ′ cos θ ′ ⎠ ⎞ tan ϕ ′ = x ′ y ′ tan 2 θ ′ = ⎝ ⎛ 0 0 1 0 − 1 0 1 0 0 ⎠ ⎞ ⎝ ⎛ cos ϕ sin θ sin ϕ sin θ cos θ ⎠ ⎞ = ⎝ ⎛ cos θ − sin ϕ sin θ cos ϕ sin θ ⎠ ⎞ = − cos θ sin ϕ sin θ = cos 2 θ ′ sin 2 θ ′ = cos 2 2 θ ′ sin 2 θ ′ cos 2 θ ′ = 1 + cos 2 2 θ ′ − sin 2 2 θ ′ 2 sin 2 θ ′ cos 2 θ ′ = 1 + cos θ ′ sin θ ′ = 1 + z ′ x ′ 2 + y ′ 2 = 1 + cos ϕ sin θ cos 2 θ + sin 2 ϕ sin 2 θ = 1 + cos ϕ sin θ 1 − cos 2 ϕ sin 2 θ = 1 + cos ϕ sin θ 1 − cos ϕ sin θ Thus, we get the same results for the angles θ ′ and ϕ ′ in both cases, so that H ≡ R x ^ + z ^ ( π ) .