Quantum Computing 2.4 -- Quantum code golf
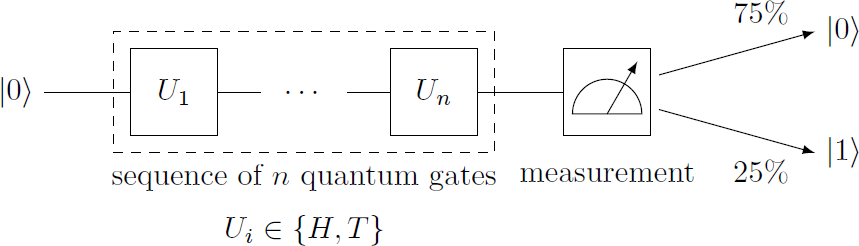
Our task is to prepare a qubit, so that we ge a state ∣ ψ ⟩ , that yields the result ∣ 0 ⟩ in 75% of cases when measured. The qubit has the initial state ∣ 0 ⟩ . Unlike before, only the quantum gates H and T are available to manipulate the qubit. The final state ∣ ψ ⟩ results from a sequence of operations: ∣ ψ ⟩ = U n ⋅ U n − 1 ⋯ U 2 ⋅ U 1 ∣ 0 ⟩ , U i ∈ { H , T } What is the minimum number n of operations needed to get a final state with ∣ ⟨ 0 ∣ ψ ⟩ ∣ 2 = 4 3 ?
Details:
The two quantum gates have in the
{
∣
0
⟩
,
∣
1
⟩
}
basis the matrix representation
 H
T
=
2
1
(
1
1
1
−
1
)
=
(
1
0
0
e
i
π
/
4
)
It may be helpful to visualize the effect of the quantum gates on the Bloch sphere (see
problem 2.3
).
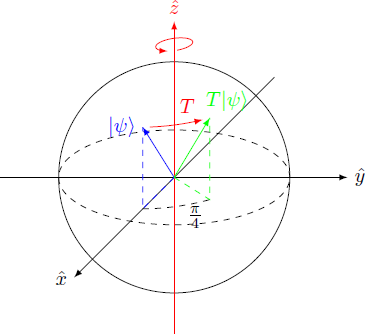
In threedimensional space, the phase shift gate
T
corresponds geometrically to a rotation around the
z
^
- axis by the angle
ϕ
=
π
/
4
.
H
T
=
2
1
(
1
1
1
−
1
)
=
(
1
0
0
e
i
π
/
4
)
It may be helpful to visualize the effect of the quantum gates on the Bloch sphere (see
problem 2.3
).
In threedimensional space, the phase shift gate
T
corresponds geometrically to a rotation around the
z
^
- axis by the angle
ϕ
=
π
/
4
.
Side note: All 1-qubit quantum gates can be represented or approximated by a sequence of operators H and T . In particular, the Pauli matrices have the representation X Y Z = H ⋅ T 4 ⋅ H = i H ⋅ T 4 ⋅ H ⋅ T 4 = T 4
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
The optimal sequence of the operators H and T must obey the following rules
We can justify the first rule by the fact, that the phase shift does not alter the probability amplitudes of the state. If the sequece ends with the operation T , we can delete this last operation without altering the measurement results. In particular, the phase shift does not alter the initial state ( T ∣ 0 ⟩ = ∣ 0 ⟩ ).
The second rule follows from the fact, that the Hadamard gate is self-adjoint so that H ⋅ H = I . If in the sequence somewhere the H operator appears twice in direct succession, then you can simply omit both operators without changing anything.
Considering these rules, we get a sequence of possible "programs" for our quantum computer: H , H T H , H T T H , H T T T H , H T H T H , … The first nontrivial seqeunces have the form H T k H . In this case, the probability P ∣ 0 ⟩ = ∣ ⟨ 0 ∣ ψ ⟩ ∣ 2 for the measurement result ∣ 0 ⟩ yields P ∣ 0 ⟩ = ∣ ⟨ 0 ∣ H T k H ∣ 0 ⟩ ∣ 2 = ∣ ∣ ∣ ∣ 2 1 ( 1 0 ) ( 1 1 1 − 1 ) ( 1 0 0 e i k 4 π ) ( 1 1 1 − 1 ) ( 1 0 ) ∣ ∣ ∣ ∣ 2 = ∣ ∣ ∣ ∣ 2 1 ( 1 1 ) ( 1 0 0 e i k 4 π ) ( 1 1 ) ∣ ∣ ∣ ∣ 2 = ∣ ∣ ∣ ∣ 2 1 + e i k 4 π ∣ ∣ ∣ ∣ 2 = 2 1 + cos 4 k π = 1 , 2 1 + 8 1 , 2 1 , 2 1 − 8 1 , 0 Note, that the wanted result P ∣ 0 ⟩ = 3 / 4 does not appear in this list.
Now we consider the next sequence H T H T H : P ∣ 0 ⟩ = ∣ ⟨ 0 ∣ H T H T H ∣ 0 ⟩ ∣ 2 = ∣ ∣ ∣ ∣ 8 1 ( 1 0 ) ( 1 1 1 − 1 ) ( 1 0 0 e i 4 π ) ( 1 1 1 − 1 ) ( 1 0 0 e i 4 π ) ( 1 1 1 − 1 ) ( 1 0 ) ∣ ∣ ∣ ∣ 2 = 8 1 ∣ ∣ ∣ ∣ ( 1 1 ) ( 1 0 0 e i 4 π ) ( 1 1 1 − 1 ) ( 1 0 0 e i 4 π ) ( 1 1 ) ∣ ∣ ∣ ∣ 2 = 8 1 ∣ ∣ ∣ ∣ ( 1 e i 4 π ) ( 1 1 1 − 1 ) ( 1 e i 4 π ) ∣ ∣ ∣ ∣ 2 = 8 1 ∣ ∣ ∣ ∣ ( 1 e i 4 π ) ( 1 + e i 4 π 1 − e i 4 π ) ∣ ∣ ∣ ∣ 2 = 8 1 ∣ ∣ 1 + 2 e i 4 π − e i 2 π ∣ ∣ 2 = 8 1 ∣ ∣ ∣ ( 2 + 1 ) + ( 2 − 1 ) i ∣ ∣ ∣ 2 = 8 1 ( ( 2 + 1 ) 2 + ( 2 − 1 ) 2 ) = 8 1 ( 2 + 1 + 2 2 + 2 + 1 − 2 2 ) = 4 3 Thus, we get the wanted probability of 75%. Futhermore, we have proved, that the sequence H T H T H with the length n = 5 is the shortest sequence with this property.
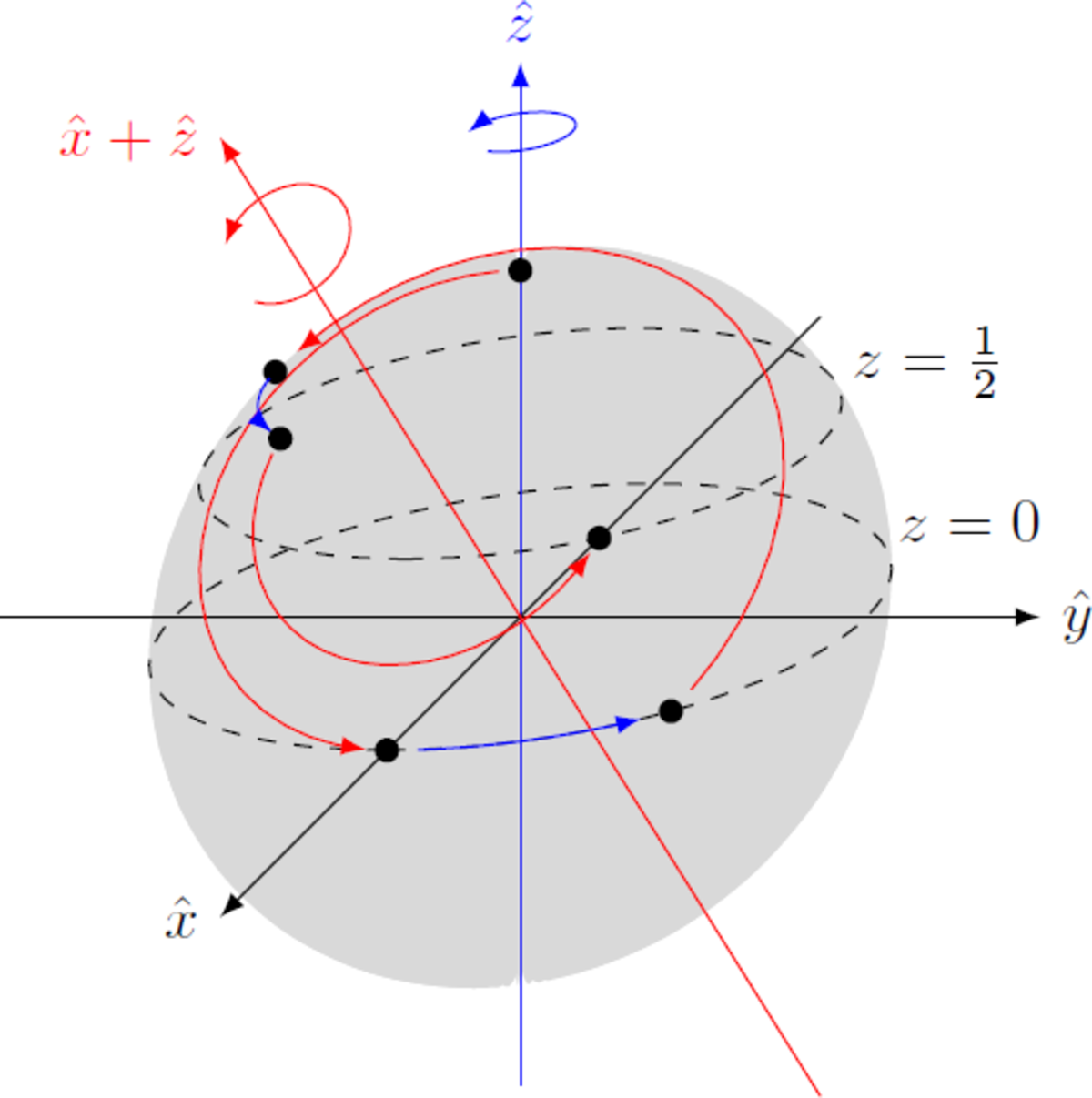
Alternatively, you can visualize these operations on the Bloch sphere. In this representation, the operator H corresponds to a rotation about the angle π around the axis x ^ + z ^ and T rotates the state vector by the angle π / 4 around the axis z ^ . We start at the point r = z ^ (north pole of the Bloch sphere). The goal is to get to a point at the circle z = cos ( θ ) = 2 cos 2 ( θ / 2 ) − 1 = 1 / 2 using only this two rotation operations. The two rotation matrices read H T = ⎝ ⎛ 0 0 1 0 − 1 0 1 0 0 ⎠ ⎞ = ⎝ ⎛ 2 1 2 1 0 − 2 1 2 1 0 0 0 1 ⎠ ⎞ The final state of the operation H T H T H results (without displaying all the calculations) H ⋅ T ⋅ H ⋅ T ⋅ H ⋅ z ^ = ⎝ ⎛ 1 / 2 1 / 2 1 / 2 ⎠ ⎞ Finally, we can visualize these operations: