Quantum Computing 2.5 -- Mirrors and beam splitters

Computer Science Level 5

Consider the following optical setup with a single photon source, two beam splitters, two mirrors and two detectors 0 and 1:

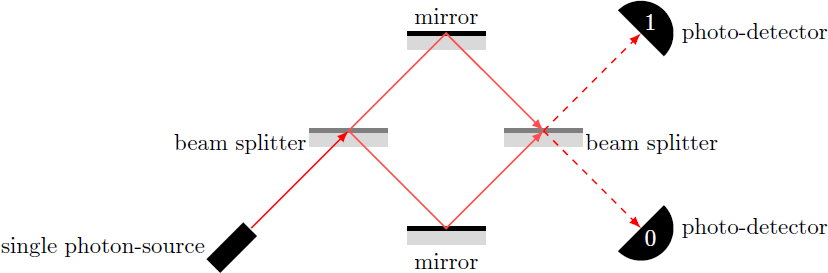
The light source now emits a single photon. What is the probability that this light particle will be measured at detector 0?

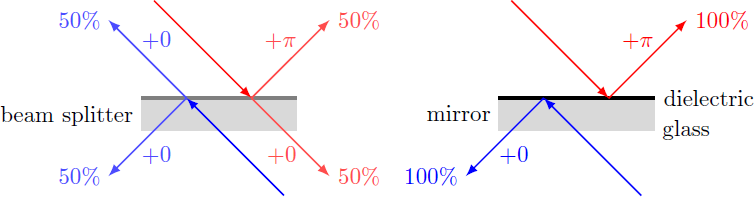
Details and assumptions: The mirrors and beam splitters consist of a glass plate coated with a dielectric film that reflects light. In the case of the beam splitter, the reflectivity and transmittity are both equal to 50%. The reflectivity of the mirror is 100%. The reflection at the air-dielectric interface leads to a phase shift by the angle π \pi . By contrast, there is no phase shift in reflection at the glass-dielectric interface and in transmission. We assume that the optical setup is lossless and that the detectors work 100% efficient.

Note: The photon may be below or above the beam splitters, so we can refer to these positions as different quantum states ∣ 0 ⟩ | 0 \rangle and ∣ 1 ⟩ | 1 \rangle . The photon starts in the state ∣ 0 ⟩ | 0 \rangle and assumes a final state ∣ 0 ⟩ | 0 \rangle , if it is measured by the detector 0. The optical setup can be considered as a 1-qubit quantum gate, which is described by an operator U U . Therefore, the wanted probability is calculated by P ∣ 0 ⟩ = ∣ ⟨ 0 ∣ U ∣ 0 ⟩ ∣ 2 P_ {| 0 \rangle} = | \langle 0 | U | 0 \rangle | ^ 2 .

Here is an older version of this problem with a more complicated setup.

0% 50% 75% 25% 100%

Markus Michelmann by Markus Michelmann , 35, Germany

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

We assign the state ∣ 0 ⟩ | 0 \rangle to a photon in the lower half, while a photon in the upper half has a state ∣ 1 ⟩ | 1 \rangle . The beam splitter generates from the base states ∣ 0 ⟩ | 0 \rangle and ∣ 1 ⟩ | 1 \rangle a uniform superposition α ∣ 0 ⟩ + β ∣ 1 ⟩ \alpha | 0 \rangle + \beta | 1 \rangle with the probabilities ∣ a l p h a ∣ 2 = ∣ β ∣ 2 = 1 2 | alpha | ^ 2 = | \beta | ^ 2 = \frac {1} {2} . For an incident beam in the state ∣ 1 ⟩ | 1 \rangle , the beam splitter produces a phase shift between reflected and transmitted beam with the phase factor e i π = − 1 e ^ {i \pi} = -1 . In the other case, however, there is no phase shift between the outgoing beams. The beam splitter thus acts as a Hadamard gate: ( beam splitter ) ∣ 0 ⟩ = ∣ 0 ⟩ + ∣ 1 ⟩ 2 ( beam splitter ) ∣ 1 ⟩ = ∣ 0 ⟩ − ∣ 1 ⟩ 2 ⇒ beam splitter ≡ H = 1 2 ( 1 1 1 − 1 ) \begin{aligned} (\text{beam splitter}) |0\rangle &= \frac{|0\rangle + |1\rangle}{\sqrt{2}} \\ (\text{beam splitter}) |1\rangle &= \frac{|0\rangle - |1\rangle}{\sqrt{2}} \\ \Rightarrow \quad \text{beam splitter} \equiv H &= \frac{1}{\sqrt{2}} \left( \begin{array}{cc} 1 & 1 \\ 1 & -1 \end{array} \right) \end{aligned} At the mirrors the light is only reflected, so that the incident photon in the state ∣ 0 ⟩ | 0 \rangle or ∣ 1 ⟩ | 1 \rangle also remains in the respective base state. Since the mirrors are oriented so that the coated side points upwards, only in the state 0 ⟩ 0 \rangle a phase shift with the phase factor e i π = − 1 e ^ {i \pi} = -1 results. Thus, the two mirrors in the { 0 ⟩ , ∣ 1 ⟩ } \{0 \rangle, | 1 \rangle \} -basis correspond to a phase flip ( Z Z -gate): ( mirrors ) ∣ 0 ⟩ = − ∣ 0 ⟩ ( mirrors ) ∣ 1 ⟩ = ∣ 1 ⟩ ⇒ mirrors ≡ − Z = ( − 1 0 0 − 1 ) \begin{aligned} (\text{mirrors}) |0\rangle &= - |0\rangle \\ (\text{mirrors}) |1\rangle &= |1\rangle \\ \Rightarrow \quad \text{mirrors} \equiv -Z &= \left( \begin{array}{cc} -1 & 0 \\ 0 & -1 \end{array} \right) \end{aligned} The entire optical setup thus corresponds to an operation: U = ( beam splitter ) ⋅ ( mirrors ) ⋅ ( beam splitter ) = H ⋅ ( − Z ) ⋅ H = − 1 2 ( 1 1 1 − 1 ) ( 1 0 0 − 1 ) ( 1 1 1 − 1 ) = − 1 2 ( 1 1 1 − 1 ) ( 1 1 − 1 1 ) = − 1 2 ( 0 2 2 0 ) = − ( 0 1 1 0 ) = − X \begin{aligned} U &= (\text{beam splitter}) \cdot (\text{mirrors}) \cdot (\text{beam splitter}) \\ &= H \cdot (- Z) \cdot H \\ &= -\frac{1}{2} \left( \begin{array}{cc} 1 & 1 \\ 1 & -1 \end{array} \right) \left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array} \right) \left( \begin{array}{cc} 1 & 1 \\ 1 & -1 \end{array} \right) \\ &= -\frac{1}{2} \left( \begin{array}{cc} 1 & 1 \\ 1 & -1 \end{array} \right) \left( \begin{array}{cc} 1 & 1 \\ -1 & 1 \end{array} \right) \\ &= -\frac{1}{2} \left( \begin{array}{cc} 0 & 2 \\ 2 & 0 \end{array} \right) \\ &= -\left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right) \\ &= - X \end{aligned} Thus, P = ∣ ⟨ 0 ∣ U ∣ 0 ⟩ ∣ 2 = ∣ ⟨ 0 ∣ X ∣ 0 ⟩ ∣ 2 = ∣ ⟨ 0 ∣ 1 ⟩ ∣ 2 = 0 P = |\langle 0 |U |0\rangle |^2 = |\langle 0 |X |0\rangle |^2 = |\langle 0 |1\rangle |^2 = 0

2 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...