Quantum Computing 3.1 -- Entangled or not?

Computer Science Level 4

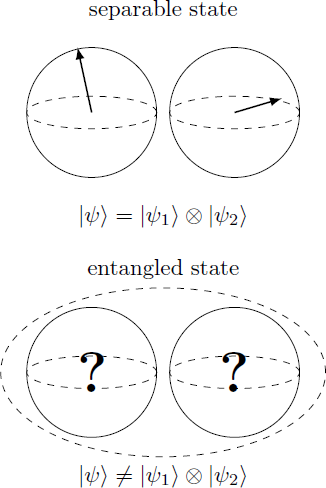
Which of the possible answers is an entangled state of a qubit pair?

Details: A qubit pair state ∣ ψ ⟩ |\psi\rangle is separable if there is a representation as a tensor product ∣ ψ 1 ⟩ ⊗ ∣ ψ 2 ⟩ |\psi_1 \rangle \otimes |\psi_2\rangle , so that ∣ ψ ⟩ = ∣ ψ 1 ⟩ ⊗ ∣ ψ 2 ⟩ = ( α 1 ∣ 0 ⟩ + β 1 ∣ 1 ⟩ ) ⊗ ( α 2 ∣ 0 ⟩ + β 2 ∣ 1 ⟩ ) = α 1 α 2 ∣ 00 ⟩ + α 1 β 2 ∣ 01 ⟩ + β 1 α 2 ∣ 10 ⟩ + β 1 β 2 ∣ 11 ⟩ α 1 , α 2 , β 1 , β 2 ∈ C \begin{aligned} |\psi\rangle &= |\psi_1 \rangle \otimes |\psi_2\rangle\\ &= (\alpha_1 |0\rangle + \beta_1 |1\rangle) \otimes (\alpha_2 |0\rangle + \beta_2|1\rangle) \\ &= \alpha_1 \alpha_2 |00\rangle + \alpha_1 \beta_2 |01\rangle + \beta_1 \alpha_2 |10\rangle + \beta_1 \beta_2 |11\rangle\\ & \alpha_1, \alpha_2, \beta_1,\beta_2 \in \mathbb{C} \end{aligned} ∣ ψ ⟩ |\psi\rangle is entangled , if such a representation is not possible. ( ∣ ψ ⟩ ≠ ∣ ψ 1 ⟩ ⊗ ∣ ψ 2 ⟩ ) (|\psi\rangle \not= |\psi_1 \rangle \otimes |\psi_2\rangle) .

1 2 ( ∣ ⁣ 00 ⟩ + i ⁣ ∣ ⁣ 01 ⟩ + i ⁣ ∣ ⁣ 10 ⟩ − ⁣ ∣ ⁣ 11 ⟩ ) \frac{1}{2} (\mid\! 00\rangle+i\!\mid\! 01\rangle+i\!\mid\! 10\rangle-\!\mid\! 11\rangle) 1 2 ( ∣ ⁣ 00 ⟩ − ⁣ ∣ ⁣ 10 ⟩ ) \frac{1}{\sqrt{2}} (\mid \! 00 \rangle - \!\mid \! 10\rangle) 1 2 ( ∣ ⁣ 00 ⟩ + ⁣ ∣ ⁣ 01 ⟩ + ⁣ ∣ ⁣ 10 ⟩ + ⁣ ∣ ⁣ 11 ⟩ ) \frac{1}{2} (\mid \! 00 \rangle+\!\mid\! 01 \rangle+\!\mid \! 10 \rangle +\!\mid\! 11\rangle) 1 2 ( ∣ ⁣ 01 ⟩ + ⁣ ∣ ⁣ 10 ⟩ ) \frac{1}{\sqrt{2}} (\mid \! 01 \rangle +\!\mid \! 10\rangle)

Markus Michelmann by Markus Michelmann , 35, Germany

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Markus Michelmann
Jul 11, 2018

For three of the four possible answers, a decomposition in single states can be found: 1 2 ( ∣ 00 ⟩ − ∣ 10 ⟩ ) = 1 2 ( ∣ 0 ⟩ − ∣ 1 ⟩ ) ⊗ ∣ 0 ⟩ 1 2 ( ∣ 00 ⟩ + ∣ 01 ⟩ + ∣ 10 ⟩ + ∣ 11 ⟩ ) = 1 2 ( ∣ 0 ⟩ + ∣ 1 ⟩ ) ⊗ 1 2 ( ∣ 0 ⟩ + ∣ 1 ⟩ ) 1 2 ( ∣ 00 ⟩ + i ∣ 01 ⟩ + i ∣ 10 ⟩ − ∣ 11 ⟩ ) = 1 2 ( ∣ 0 ⟩ + i ∣ 1 ⟩ ) ⊗ 1 2 ( ∣ 0 ⟩ + i ∣ 1 ⟩ ) \begin{aligned} \frac{1}{\sqrt{2}} (|00\rangle - |10\rangle) &= \frac{1}{\sqrt{2}} (|0\rangle - |1\rangle) \otimes |0\rangle \\ \frac{1}{2} (|00\rangle + |01\rangle + |10\rangle + |11\rangle) &= \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle) \otimes \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle) \\ \frac{1}{2} (|00\rangle +i |01\rangle + i|10\rangle - |11\rangle) &= \frac{1}{\sqrt{2}}(|0\rangle +i |1\rangle) \otimes \frac{1}{\sqrt{2}}(|0\rangle +i |1\rangle) \end{aligned} We are now trying to represent the fourth state as a tensor product 1 2 ( ∣ 01 ⟩ + ∣ 10 ⟩ ) = ! α 1 α 2 ∣ 00 ⟩ + α 1 β 2 ∣ 01 ⟩ + β 1 α 2 ∣ 10 ⟩ + β 1 β 2 ∣ 11 ⟩ ⇒ α 1 α 2 = 0 and β 1 β 2 = 0 ⇒ α 1 or α 2 = 0 and β 1 or β 2 = 0 ⇒ α 1 β 2 = 0 or β 1 α 2 = 0 ⇒ ∣ ψ ⟩ = ∣ 01 ⟩ or ∣ ψ ⟩ = ∣ 10 ⟩ \begin{aligned} & & \frac{1}{\sqrt{2}}(|01\rangle + |10\rangle) &\stackrel{!}{=} \alpha_1 \alpha_2 |00\rangle + \alpha_1 \beta_2 |01\rangle + \beta_1 \alpha_2 |10\rangle + \beta_1 \beta_2 |11\rangle \\ \Rightarrow & & \alpha_1 \alpha_2 = 0 \quad &\text{and} \quad \beta_1 \beta_2 = 0 \\ \Rightarrow & & \alpha_1 \text{ or } \alpha_2 = 0 \quad &\text{and} \quad \beta_1 \text{ or } \beta_2 = 0\\ \Rightarrow & & \alpha_1 \beta_2 = 0 \quad &\text{or} \quad \beta_1 \alpha_2 = 0 \\ \Rightarrow & & |\psi\rangle = |01\rangle \quad &\text{or} \quad |\psi\rangle = |10\rangle \end{aligned} Thus we receive a contradiction. Therefore, this state must be entangled. In particular, this state has the special name ∣ Ψ + ⟩ |\Psi +\rangle and belongs to the four Bell states ∣ Φ ± ⟩ = 1 2 ( ∣ 00 ⟩ ± ∣ 11 ⟩ ) ∣ Ψ ± ⟩ = 1 2 ( ∣ 01 ⟩ ± ∣ 10 ⟩ ) \begin{aligned} |\Phi_\pm\rangle &= \frac{1}{\sqrt{2}}(|00\rangle \pm |11\rangle) \\ |\Psi_\pm\rangle &= \frac{1}{\sqrt{2}}(|01\rangle \pm |10\rangle) \end{aligned} which are all maximally entangled.

2 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...