Quantum Computing 3.2 -- Measurement of a Bell pair

Computer Science Level 4

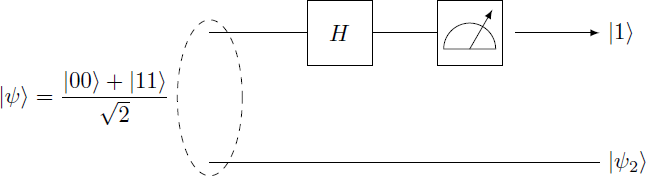
A qubit pair is initially in the Bell state ∣ ψ ⟩ = 1 2 ( ∣ 00 ⟩ + ∣ 11 ⟩ ) |\psi\rangle = \frac{1}{\sqrt{2}}(|00\rangle + |11\rangle) . Now the Hadamard gate H H is applied to the first qubit and then it is measured. In our case, the result of this measurement is ∣ 1 ⟩ |1\rangle .

In which state is the second qubit ∣ ψ 2 ⟩ |\psi_2\rangle after the measurement?

Details: The Hadamard gate is given in the basis { ∣ 0 ⟩ , ∣ 1 ⟩ } \{|0\rangle,|1\rangle\} by the matrix H = 1 2 ( 1 1 1 − 1 ) H = \frac{1}{\sqrt{2}} \left( \begin{array}{cc} 1 & 1 \\ 1 & - 1 \end{array} \right)

∣ 1 ⟩ \mid 1\rangle ∣ 0 ⟩ \mid 0\rangle ∣ ⁣ + ⟩ = ∣ 0 ⟩ + ∣ 1 ⟩ 2 \mid\!+\rangle = \frac{\mid 0\rangle+\mid 1\rangle}{\sqrt 2} ∣ ⁣ − ⟩ = ∣ 0 ⟩ − ∣ 1 ⟩ 2 \mid\!-\rangle = \frac{\mid 0\rangle-\mid 1\rangle}{\sqrt 2}

Markus Michelmann by Markus Michelmann , 35, Germany

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Markus Michelmann
Jul 11, 2018

The Hadamard operation acts only on the first qubit: H 1 ∣ ψ ⟩ = ( H ⊗ I ) 1 2 ( ∣ 00 ⟩ + ∣ 11 ⟩ ) = 1 2 ( H ∣ 0 ⟩ ⊗ I ∣ 0 ⟩ + H ∣ 1 ⟩ ⊗ I ∣ 1 ⟩ ) = 1 2 ( 1 2 ( ∣ 0 ⟩ + ∣ 1 ⟩ ) ⊗ ∣ 0 ⟩ + 1 2 ( ∣ 0 ⟩ − ∣ 1 ⟩ ) ⊗ ∣ 1 ⟩ ) = 1 2 ( ∣ 00 ⟩ + ∣ 01 ⟩ + ∣ 10 ⟩ − ∣ 11 ⟩ ) = 1 2 ( ∣ 0 ⟩ ⊗ ( ∣ 0 ⟩ + ∣ 1 ⟩ ) + ∣ 1 ⟩ ⊗ ( ∣ 0 ⟩ − ∣ 1 ⟩ ) ) = 1 2 ( ∣ 0 ⟩ ⊗ ∣ + ⟩ + ∣ 1 ⟩ ⊗ ∣ − ⟩ ) \begin{aligned} H_1|\psi\rangle &= (H \otimes I) \frac{1}{\sqrt{2}} \left( |00\rangle + |11\rangle \right) \\ &= \frac{1}{\sqrt{2}} \left( H |0\rangle \otimes I |0\rangle + H |1\rangle \otimes I |1\rangle \right) \\ &= \frac{1}{\sqrt{2}} \left(\frac{1}{\sqrt{2}} \left(|0\rangle + |1\rangle \right) \otimes |0\rangle + \frac{1}{\sqrt{2}} \left(|0\rangle - |1\rangle \right) \otimes |1\rangle \right) \\ &= \frac{1}{2} \left( |00\rangle + |01\rangle + |10\rangle - |11\rangle \right) \\ &= \frac{1}{2} \left( |0\rangle \otimes (|0\rangle + |1\rangle) + |1\rangle \otimes (|0\rangle - |1\rangle) \right) \\ &= \frac{1}{\sqrt{2}} \left( |0\rangle \otimes |+\rangle + |1\rangle \otimes |-\rangle \right) \end{aligned} Note that this is still an entangled state. Only when measuring this entanglement is destroyed and we get of the measurement result ∣ 1 ⟩ | 1 \rangle the overall state ∣ ψ ′ ⟩ = ∣ 1 ⟩ ⊗ ∣ − ⟩ |\psi'\rangle = |1\rangle \otimes |-\rangle Therefore, the second qubit is in the state ∣ ψ 2 ⟩ = ∣ − ⟩ |\psi_2 \rangle= |-\rangle after the measurement.

Alternative solution: Alternatively, one can also represent the Bell state in the { ∣ + ⟩ , ∣ − ⟩ } \{|+\rangle, | -\rangle\} basis. A Hadamard operation corresponds to a basis transformation between { ∣ 0 ⟩ , ∣ 1 ⟩ } \{|0\rangle, |1\rangle\} and { ∣ + ⟩ , ∣ − ⟩ } \{|+\rangle, |-\rangle\} . Thus, in our experiment, the first qubit is actually measured in the base { ∣ + ⟩ , ∣ − ⟩ } \{|+\rangle, |-\rangle\} . The result ∣ 1 ⟩ |1\rangle therefore corresponds to the state H ∣ 1 ⟩ = ∣ − ⟩ H|1\rangle = |-\rangle . The measurement therefore corresponds to the application of a projection operator P = ∣ − ⟩ ⟨ − ∣ ⊗ I P = |-\rangle \langle -| \otimes I P ∣ ψ ⟩ = ( ∣ − ⟩ ⟨ − ∣ ⊗ I ) 1 2 ( ∣ 00 ⟩ + ∣ 11 ⟩ ) = 1 2 ( ⟨ − ∣ 0 ⟩ ∣ − ⟩ ⊗ ∣ 0 ⟩ + ⟨ − ∣ 1 ⟩ ∣ − ⟩ ⊗ ∣ 1 ⟩ ) = 1 2 ( 1 2 ( ⟨ 0 ∣ − ⟨ 1 ∣ ) ∣ 0 ⟩ ∣ − ⟩ ⊗ ∣ 0 ⟩ + 1 2 ( ⟨ 0 ∣ − ⟨ 1 ∣ ) ∣ 1 ⟩ ∣ − ⟩ ⊗ ∣ 1 ⟩ ) = 1 2 ⋅ 1 2 ( ∣ − ⟩ ⊗ ∣ 0 ⟩ − ∣ − ⟩ ⊗ ∣ 1 ⟩ ) = 1 2 ∣ − ⟩ ⊗ 1 2 ( ∣ 0 ⟩ − ∣ 1 ⟩ ) = 1 2 ∣ − ⟩ ⊗ ∣ − ⟩ \begin{aligned} P |\psi\rangle &= (|-\rangle \langle -| \otimes I) \frac{1}{\sqrt 2} (|00\rangle + |11\rangle) \\ &= \frac{1}{\sqrt 2} (\langle - |0\rangle |-\rangle \otimes |0\rangle + \langle - |1\rangle |-\rangle \otimes |1\rangle) \\ &= \frac{1}{\sqrt 2} \left( \frac{1}{\sqrt 2} (\langle 0 | - \langle 1|) |0\rangle |-\rangle \otimes |0\rangle + \frac{1}{\sqrt 2} (\langle 0 | - \langle 1|) |1\rangle |-\rangle \otimes |1\rangle\right) \\ &= \frac{1}{\sqrt 2} \cdot \frac{1}{\sqrt 2} (|-\rangle \otimes |0\rangle - |-\rangle \otimes |1\rangle) \\ &= \frac{1}{\sqrt 2} |-\rangle \otimes \frac{1}{\sqrt 2} \left(|0\rangle - |1\rangle\right) \\ &= \frac{1}{\sqrt 2} |-\rangle \otimes |-\rangle \end{aligned} Again, the second qubit is in the state ∣ − ⟩ |-\rangle after the measurement.

4 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...