Quantum Computing 3.4 -- Copy a quantum state
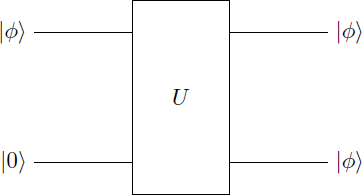
A qubit is in the state A second qubit has the initial state . We are looking for two-qubit-gate , which copies the state to the second qubit. Thus, for all one-qubit states the following should apply Is there such a quantum gate that can copy any state of a qubit?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We assume, that there is a quantum gate U with the property U ∣ ϕ ⟩ ⊗ ∣ 0 ⟩ = ∣ ϕ ⟩ ⊗ ∣ ϕ ⟩ . If we apply U on the basis states ∣ 0 0 ⟩ and 1 0 ⟩ we get the results U ∣ 0 0 ⟩ U ∣ 1 0 ⟩ = U ∣ 0 ⟩ ⊗ ∣ 0 ⟩ = ∣ 0 ⟩ ⊗ ∣ 0 ⟩ = ∣ 0 0 ⟩ ( 1 ) = U ∣ 1 ⟩ ⊗ ∣ 0 ⟩ = ∣ 1 ⟩ ⊗ ∣ 1 ⟩ = ∣ 1 1 ⟩ ( 2 ) Now we consinder the case, that the first qubit is given by a superpositon ∣ + ⟩ = ( ∣ 0 ⟩ + ∣ 1 ⟩ ) / 2 . We calculate U ∣ + ⟩ ⊗ ∣ 0 ⟩ with the help of ( 1 ) and ( 2 ) : U ∣ + ⟩ ⊗ ∣ 0 ⟩ = U 2 1 ( ∣ 0 ⟩ + ∣ 1 ⟩ ) ⊗ ∣ 0 ⟩ = U 2 1 ( ∣ 0 0 ⟩ + ∣ 1 0 ⟩ ) = 2 1 ( U ∣ 0 0 ⟩ + U ∣ 1 0 ⟩ ) = 2 1 ( ∣ 0 0 ⟩ + ∣ 1 1 ⟩ ) ( 3 ) ∣ U is linear ∣ ( 1 ) and ( 2 ) We used the fact, that U is a linear operatior (i.e. U ( α ∣ ϕ ⟩ + β ∣ ψ ⟩ ) = α U ∣ ϕ ⟩ + β U ∣ ψ ⟩ ). This is true, because matrix multiplication is linear. Now we calculate the tensor product of the state ∣ + ⟩ : ∣ + ⟩ ⊗ ∣ + ⟩ = 2 1 ( ∣ 0 ⟩ + ∣ 1 ⟩ ) ⊗ 2 1 ( ∣ 0 ⟩ + ∣ 1 ⟩ ) = 2 1 ( ∣ 0 ⟩ ⊗ ( ∣ 0 ⟩ + ∣ 1 ⟩ ) + ∣ 1 ⟩ ⊗ ( ∣ 0 ⟩ + ∣ 1 ⟩ ) ) = 2 1 ( ∣ 0 ⟩ ⊗ ∣ 0 ⟩ + ∣ 0 ⟩ ⊗ ∣ 1 ⟩ + ∣ 1 ⟩ ⊗ ∣ 0 ⟩ + ∣ 1 ⟩ ⊗ ∣ 1 ⟩ ) ) = 2 1 ( ∣ 0 0 ⟩ + ∣ 0 1 ⟩ + ∣ 1 0 ⟩ + ∣ 1 1 ⟩ ) ) ( 4 ) Obviously, we get different results in ( 3 ) and ( 4 ) , so that U ∣ + ⟩ ⊗ ∣ 0 ⟩ = ( 3 ) 2 1 ( ∣ 0 0 ⟩ + ∣ 1 1 ⟩ ) = 2 1 ( ∣ 0 0 ⟩ + ∣ 0 1 ⟩ + ∣ 1 0 ⟩ + ∣ 1 1 ⟩ ) ) = ( 4 ) ∣ + ⟩ ⊗ ∣ + ⟩ in contradiction to our assumption U ∣ ψ ⟩ ∣ 0 ⟩ = ∣ ψ ⟩ ∣ ψ ⟩ . Therefore, an operator U , that can copy any quantum state, does not exist. This fact is called No-Cloning-Theorem .
In conclusion, there is no copy operation for qubits in total contrast to classical bits, which can be copied.