Quantum Computing 3.5 -- Transformed CNOT
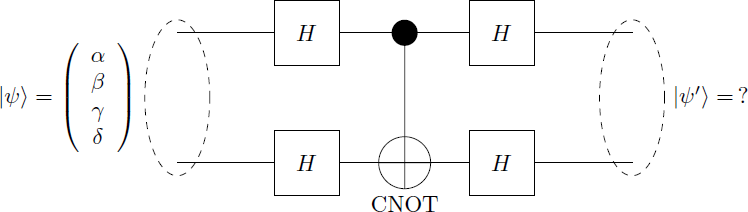 A qubit pair is intially in the state
∣
ψ
⟩
=
α
∣
0
0
⟩
+
β
∣
0
1
⟩
+
γ
∣
1
0
⟩
+
δ
∣
1
1
⟩
≡
⎝
⎜
⎜
⎛
α
β
γ
δ
⎠
⎟
⎟
⎞
∈
C
4
Now we apply a CNOT gate that has undergone a Hadamard transformation, so that we have an operation
∣
ψ
′
⟩
=
(
H
⊗
H
)
⋅
CNOT
⋅
(
H
⊗
H
)
∣
ψ
⟩
What is the corresponding vector of the state
∣
ψ
′
⟩
?
A qubit pair is intially in the state
∣
ψ
⟩
=
α
∣
0
0
⟩
+
β
∣
0
1
⟩
+
γ
∣
1
0
⟩
+
δ
∣
1
1
⟩
≡
⎝
⎜
⎜
⎛
α
β
γ
δ
⎠
⎟
⎟
⎞
∈
C
4
Now we apply a CNOT gate that has undergone a Hadamard transformation, so that we have an operation
∣
ψ
′
⟩
=
(
H
⊗
H
)
⋅
CNOT
⋅
(
H
⊗
H
)
∣
ψ
⟩
What is the corresponding vector of the state
∣
ψ
′
⟩
?
Details: The operators H and CNOT are given in the standard basis by the following matrices H CNOT = 2 1 ( 1 1 1 − 1 ) = ⎝ ⎜ ⎜ ⎛ 1 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0 ⎠ ⎟ ⎟ ⎞
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We first calculate the tensor product of the Hadamard operators H ⊗ H = ( H ⊗ I ) ⋅ ( I ⊗ H ) = 2 1 ⎝ ⎜ ⎜ ⎛ 1 0 1 0 0 1 0 1 1 0 − 1 0 0 1 0 − 1 ⎠ ⎟ ⎟ ⎞ ⋅ 2 1 ⎝ ⎜ ⎜ ⎛ 1 1 0 0 1 − 1 0 0 0 0 1 1 0 0 1 − 1 ⎠ ⎟ ⎟ ⎞ = 2 1 ⎝ ⎜ ⎜ ⎛ 1 1 1 1 1 − 1 1 − 1 1 1 − 1 − 1 1 − 1 − 1 1 ⎠ ⎟ ⎟ ⎞ We consider the whole quantum circuit as an operator U which results as matrix muliplication of the different operators U = ( H ⊗ H ) ⋅ CNOT ⋅ ( H ⊗ H ) = 4 1 ⎝ ⎜ ⎜ ⎛ 1 1 1 1 1 − 1 1 − 1 1 1 − 1 − 1 1 − 1 − 1 1 ⎠ ⎟ ⎟ ⎞ ⋅ ⎝ ⎜ ⎜ ⎛ 1 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0 ⎠ ⎟ ⎟ ⎞ ⋅ ⎝ ⎜ ⎜ ⎛ 1 1 1 1 1 − 1 1 − 1 1 1 − 1 − 1 1 − 1 − 1 1 ⎠ ⎟ ⎟ ⎞ = 4 1 ⎝ ⎜ ⎜ ⎛ 1 1 1 1 1 − 1 1 − 1 1 1 − 1 − 1 1 − 1 − 1 1 ⎠ ⎟ ⎟ ⎞ ⋅ ⎝ ⎜ ⎜ ⎛ 1 1 1 1 1 − 1 − 1 1 1 1 − 1 − 1 1 − 1 1 − 1 ⎠ ⎟ ⎟ ⎞ = ⎝ ⎜ ⎜ ⎛ 1 0 0 0 0 0 0 1 0 0 1 0 0 1 0 0 ⎠ ⎟ ⎟ ⎞ = CNOT 2 1 The whole circuit can be represented by an CNOT gate CNOT 2 1 in which control and target qubit are interchanged. For distinction we label the ordenary CNOT gate with CNOT 1 2 ≡ CNOT . The effect of these gates on the basis states is CNOT 1 2 ∣ i j ⟩ CNOT 2 1 ∣ i j ⟩ = ∣ i , i ⊕ j ⟩ = ∣ i ⊕ j , j ⟩ where i , j ∈ { 0 , 1 } . By appling the CNOT 2 1 gate on an general state vector, we get the result CNOT 2 1 ⎝ ⎜ ⎜ ⎛ α β γ δ ⎠ ⎟ ⎟ ⎞ = ⎝ ⎜ ⎜ ⎛ 1 0 0 0 0 0 0 1 0 0 1 0 0 1 0 0 ⎠ ⎟ ⎟ ⎞ ⎝ ⎜ ⎜ ⎛ α β γ δ ⎠ ⎟ ⎟ ⎞ = ⎝ ⎜ ⎜ ⎛ α δ γ β ⎠ ⎟ ⎟ ⎞