Quantum Computing 3.6 -- Triple CNOT

Computer Science Level 4

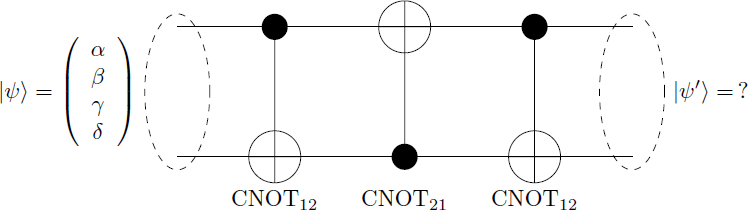
A qubit pair has the initial state ∣ ψ ⟩ = α ∣ 00 ⟩ + β ∣ 01 ⟩ + γ ∣ 10 ⟩ + δ ∣ 11 ⟩ ≡ ( α β γ δ ) ∈ C 4 |\psi\rangle = \alpha |00\rangle + \beta |01\rangle + \gamma |10\rangle + \delta |11\rangle \equiv \left( \begin{array}{c} \alpha \\ \beta \\ \gamma\\ \delta \end{array} \right) \in \mathbb{C}^4 Three controlled NOT gates are applied on this initial state: ∣ ψ ′ ⟩ = CNOT 12 ⋅ CNOT 21 ⋅ CNOT 12 ∣ ψ ⟩ |\psi'\rangle = \text{CNOT}_{12} \cdot \text{CNOT}_{21} \cdot \text{CNOT}_{12} |\psi\rangle What is the result of the state vector of the final state ∣ ψ ′ ⟩ |\psi'\rangle ?

Details: The gates CNOT 12 _{12} and CNOT 21 _{21} differ in that control and target qubits are reversed. The application of these gates to the basis states results ∣ ψ ⟩ CNOT 12 ∣ ψ ⟩ CNOT 21 ∣ ψ ⟩ ∣ 00 ⟩ ∣ 00 ⟩ ∣ 00 ⟩ ∣ 01 ⟩ ∣ 01 ⟩ ∣ 11 ⟩ ∣ 10 ⟩ ∣ 11 ⟩ ∣ 10 ⟩ ∣ 11 ⟩ ∣ 10 ⟩ ∣ 01 ⟩ \begin{array}{c|cc} |\psi\rangle & \text{CNOT}_{12} |\psi\rangle & \text{CNOT}_{21} |\psi\rangle\\ \hline |00\rangle & |00\rangle & |00\rangle \\ |01\rangle & |01\rangle & |11\rangle \\ |10\rangle & |11\rangle & |10\rangle \\ |11\rangle & |10\rangle & |01\rangle \end{array}

( δ β γ α ) \left( \begin{array}{c} \delta \\ \beta \\ \gamma \\ \alpha \end{array}\right) ( α δ γ β ) \left( \begin{array}{c} \alpha \\ \delta \\ \gamma \\ \beta \end{array}\right) ( α γ β δ ) \left( \begin{array}{c} \alpha \\ \gamma \\ \beta \\ \delta \end{array}\right) ( δ γ β α ) \left( \begin{array}{c} \delta \\ \gamma \\ \beta \\ \alpha \end{array}\right) ( α β δ γ ) \left( \begin{array}{c} \alpha \\ \beta \\ \delta \\ \gamma \end{array}\right)

Markus Michelmann by Markus Michelmann , 35, Germany

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Markus Michelmann
Jul 12, 2018

From the table we can read the matrix representation of the operators. The columns of the matrix correspond exactly to the vectors CNOT ∣ i j ⟩ \text{CNOT}|ij\rangle : CNOT 12 = ( CNOT 12 ∣ 00 ⟩ , CNOT 12 ∣ 01 ⟩ , CNOT 12 ∣ 10 ⟩ , CNOT 12 ∣ 11 ⟩ ) = ( 1 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0 ) CNOT 21 = ( CNOT 21 ∣ 00 ⟩ , CNOT 21 ∣ 01 ⟩ , CNOT 21 ∣ 10 ⟩ , CNOT 21 ∣ 11 ⟩ ) = ( 1 0 0 0 0 0 0 1 0 0 1 0 0 1 0 0 ) \begin{aligned} \text{CNOT}_{12} &= \left( \text{CNOT}_{12}|00\rangle, \text{CNOT}_{12}|01\rangle, \text{CNOT}_{12}|10\rangle, \text{CNOT}_{12}|11\rangle \right) = \left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{array} \right)\\ \text{CNOT}_{21} &= \left( \text{CNOT}_{21}|00\rangle, \text{CNOT}_{21}|01\rangle, \text{CNOT}_{21}|10\rangle, \text{CNOT}_{21}|11\rangle \right) = \left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \end{array} \right) \end{aligned} The overall operator of the circuit is given by matrix multiplication U = CNOT 12 ⋅ CNOT 21 ⋅ CNOT 12 = ( 1 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0 ) ⋅ ( 1 0 0 0 0 0 0 1 0 0 1 0 0 1 0 0 ) ⋅ ( 1 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0 ) = ( 1 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0 ) ⋅ ( 1 0 0 0 0 0 1 0 0 0 0 1 0 1 0 0 ) = ( 1 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 ) = SWAP \begin{aligned} U &= \text{CNOT}_{12} \cdot \text{CNOT}_{21} \cdot \text{CNOT}_{12} \\ &= \left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{array} \right) \cdot \left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \end{array} \right) \cdot \left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{array} \right) \\ &= \left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{array} \right) \cdot \left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \end{array} \right) \\ &= \left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right)\\ &= \text{SWAP} \end{aligned} The result is the SWAP gate which, when applied to a separable state, swaps the individual states: SWAP ∣ ψ 1 ⟩ ⊗ ∣ ψ 2 ⟩ = ∣ ψ 2 ⟩ ⊗ ∣ ψ 1 ⟩ \text{SWAP}|\psi_1 \rangle \otimes |\psi_2\rangle = |\psi_2\rangle \otimes |\psi_1\rangle For an general state vector we get the result SWAP ∣ ψ ⟩ = ( 1 0 0 0 0 0 1 0 0 1 0 0 0 0 0 1 ) ( α β γ δ ) = ( α γ β δ ) \text{SWAP} |\psi\rangle = \left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right) \left( \begin{array}{c} \alpha \\ \beta \\ \gamma \\ \delta \end{array} \right) = \left( \begin{array}{c} \alpha \\ \gamma \\ \beta \\ \delta \end{array} \right)

3 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...