Quantum Tunnelling

Classical Mechanics Level 5

A one-dimensional "universe" consists of the linear space between x = 0 x = 0 and x = x f x = x_f (see below). There is a single particle in this universe, and its behavior is governed by a variant of the time-independent Schrodinger equation, expressed in terms of a non-unitary wave function Ψ N ( x ) \Psi_N (x) .

The quantities V V and E E are the potential energy and total energy, respectively.

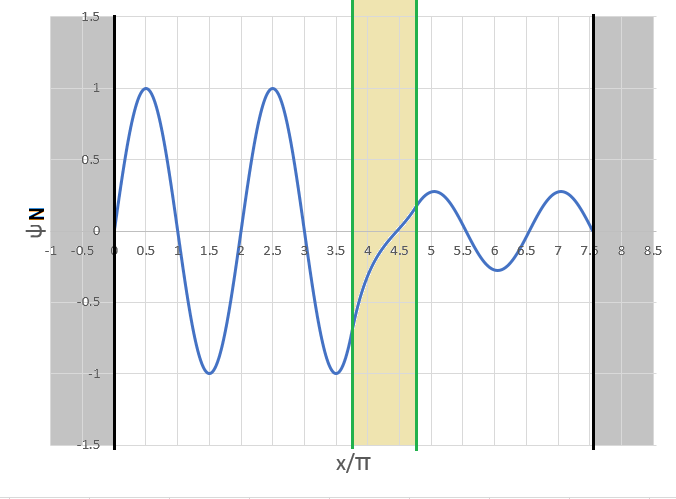
− d 2 d x 2 Ψ N ( x ) + V ( x ) Ψ N ( x ) = E Ψ N ( x ) \large{-\frac{d^2}{d x^2} \, \Psi_N (x) + V(x) \, \Psi_N (x) = E \, \Psi_N (x)}

Let us consider a case in which E = 1 E = 1 . The particle is situated inside an infinite potential well, which contains a finite potential region (see graphic). The potential varies as follows:

V ( x ) = ∞ x < 0 V ( x ) = 0 0 ≤ x < x 1 V ( x ) = 1.95 x 1 ≤ x < x 2 V ( x ) = 0 x 2 ≤ x ≤ x f V ( x ) = ∞ x > x f x 1 = 15 4 π x 2 = 19 4 π x f ≈ 7.55 π (a zero crossing of Ψ N ( x ) ) V (x) = \infty \,\,\,\,\,\,\,\, x < 0 \\ V (x) = 0 \,\,\,\,\,\,\,\, 0 \leq x < x_1 \\ V (x) = 1.95 \,\,\,\,\,\,\,\, x_1 \leq x < x_2 \\ V (x) = 0 \,\,\,\,\,\,\,\, x_2 \leq x \leq x_f \\ V (x) = \infty \,\,\,\,\,\,\,\, x > x_f \\ x_1 = \frac{15}{4} \pi \\ x_2 = \frac{19}{4} \pi \\ x_f \approx 7.55 \pi \, \text{(a zero crossing of } \Psi_N (x))

The values of Ψ N ( x ) \Psi_N (x) and its first spatial derivative at x = 0 x = 0 are (see graphic):

Ψ N ( 0 ) = 0 ( d d x Ψ N ) ( 0 ) = 1 \Psi_N (0) = 0 \\ \Big ( \frac{d}{dx} \, \Psi_N \Big ) (0) = 1

Note that the potential energy V ( x ) V(x) exceeds E E inside the finite-potential region, and yet the particle still has a finite non-zero probability of being measured anywhere inside the infinite well (except for the extreme boundaries).

The probability of detecting the particle within the region a ≤ x ≤ b a \leq x \leq b is:

P ( a ≤ x ≤ b ) = ∫ a b ∣ Ψ N ( x ) ∣ 2 d x ∫ 0 x f ∣ Ψ N ( x ) ∣ 2 d x \large{P(a \leq x \leq b) = \frac{\int_a^b |\Psi_N (x)|^2 \, dx }{\int_0^{x_f} |\Psi_N (x)|^2 \, dx }}

What is the probability of detecting the particle in the region ( x 2 ≤ x ≤ x f ) ( x_2 \leq x \leq x_f ) ?

Note: This problem lends itself well to numerical solution


The answer is 0.05276.

Steven Chase by Steven Chase , 37, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Mark Hennings
Jan 19, 2019

The wave function is Ψ ( x ) = { 0 x < 0 sin ⁡ x 0 < x < x 1 A e κ ( x − x 1 ) + B e − κ ( x − x 1 ) x 1 < x < x 2 C sin ⁡ x + D cos ⁡ x x 2 < x < x f 0 x > x f \Psi(x) \; = \; \left\{ \begin{array}{lll}0 & \hspace{2cm} & x < 0 \\ \sin x & & 0 < x < x_1 \\ Ae^{\kappa(x-x_1)} + Be^{-\kappa(x-x_1)} & & x_1 < x < x^2 \\ C\sin x + D\cos x & & x_2 < x < x_f \\ 0 & & x > x_f \end{array}\right. where κ 2 = 0.95 \kappa^2 = 0.95 and A , B , C , D A,B,C,D are to be chosen to that Ψ \Psi and Ψ ′ \Psi' are continuous for 0 < x < x f 0 < x < x_f . Thus we need to solve the simultaneous equations sin ⁡ x 1 = A + B C sin ⁡ x 2 + D cos ⁡ x 2 = A e κ π + B e κ π cos ⁡ x 1 = κ A − κ B C cos ⁡ x 2 − D sin ⁡ x 2 = κ A e κ π − κ B e − κ π \begin{array}{rclcrcl} \sin x_1 &= & A + B & \hspace{2cm} & C\sin x_2 + D\cos x_2 & = & Ae^{\kappa \pi} + Be^{\kappa \pi} \\ \cos x_1 &=& \kappa A - \kappa B & & C\cos x_2 - D\sin x_2 & = & \kappa Ae^{\kappa \pi} - \kappa Be^{-\kappa \pi} \end{array} obtaining A = 0.00918473 B = − 0.716292 C = − 0.0432851 D = − 0.273480 A \; = \; 0.00918473 \hspace{1cm} B \; = \; -0.716292 \hspace{1cm} C \; = \; -0.0432851 \hspace{1cm} D \; = \; -0.273480 and hence the zero of Ψ \Psi near 7.55 π 7.55\pi is x f = 23.7189 x_f = 23.7189 .

It is now easy to calculate ∫ 0 x f ∣ Ψ ( x ) ∣ 2 d x = 6.73691 ∫ x 2 x f ∣ Ψ ( x ) ∣ 2 d x = 0.355416 \int_0^{x_f} |\Psi(x)|^2\,dx \; = \; 6.73691 \hspace{2cm} \int_{x_2}^{x_f} |\Psi(x)|^2\,dx \; = \; 0.355416 making the desired probability 0.0527565 \boxed{0.0527565} .

1 Helpful 1 Interesting 1 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...