Quantum Well - Ramp Potential

A particle in a one-dimensional quantum well is governed by a variant of the time-independent Schrodinger equation, expressed in terms of a non-normalized wave function $\Psi_N (x)$ .

The quantities $V$ and $E$ are the potential energy and total energy, respectively.

$\large{-\frac{d^2}{d x^2} \, \Psi_N (x) + V(x) \, \Psi_N (x) = E \, \Psi_N (x)}$

Let us consider a case in which $E = 2.5$ . The potential varies as follows:

$V (x) = \infty \,\,\,\,\,\,\,\, x < 0 \\ V (x) = x \,\,\,\,\,\,\,\, 0 \leq x \leq x_f \\ V (x) = \infty \,\,\,\,\,\,\,\, x > x_f \\ x_f \approx 3.0267 \, \text{(a zero crossing of } \Psi_N (x))$

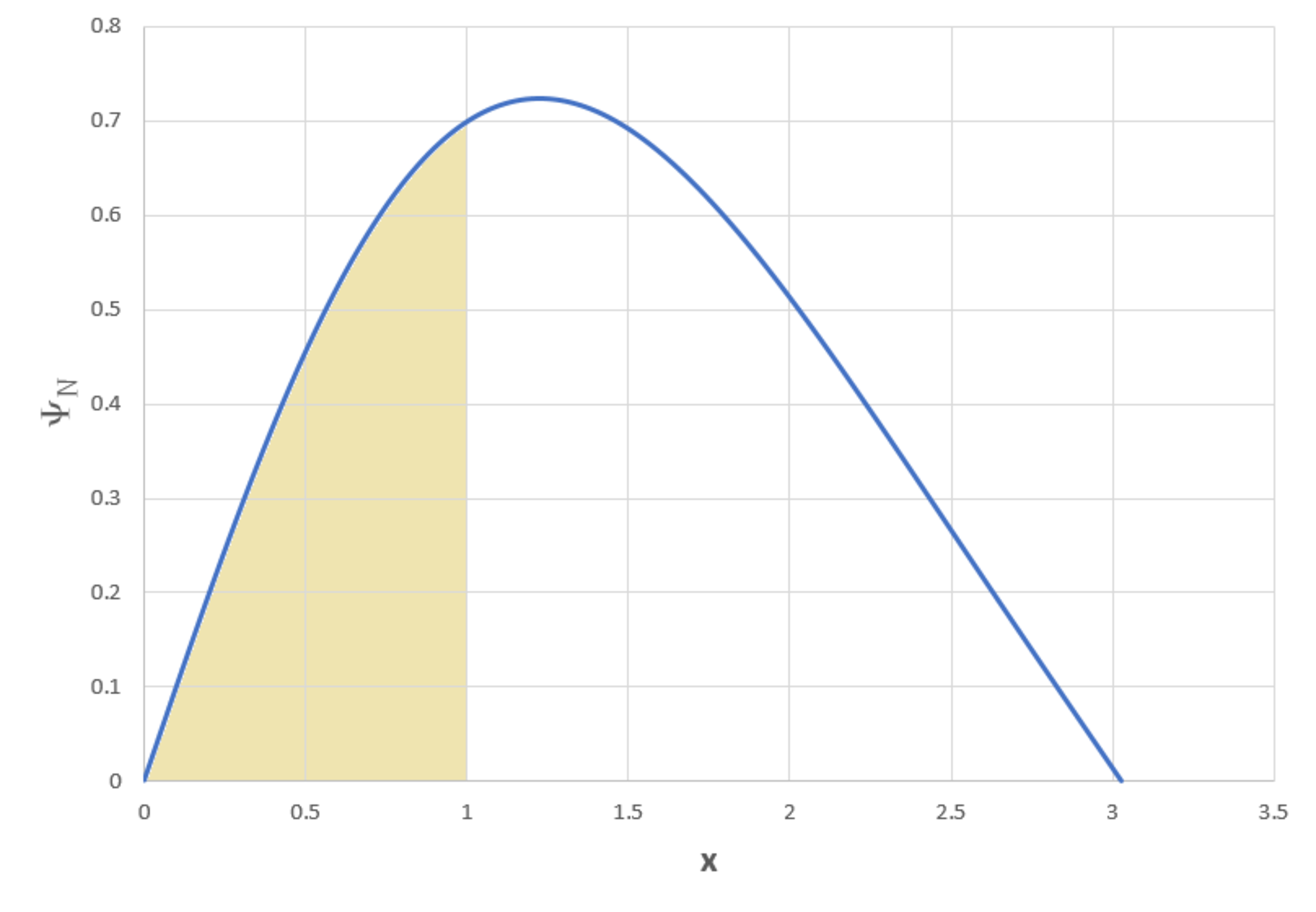
The values of $\Psi_N (x)$ and its first spatial derivative at $x = 0$ are (see graphic):

$\Psi_N (0) = 0 \\ \Big ( \frac{d}{dx} \, \Psi_N \Big ) (0) = 1$

Note that the potential energy $V(x)$ exceeds $E$ for $x > 2.5$ , and yet the particle still has a finite non-zero probability of being measured anywhere inside the well.

The probability of detecting the particle within the region $a \leq x \leq b$ is:

$\large{P(a \leq x \leq b) = \frac{\int_a^b |\Psi_N (x)|^2 \, dx }{\int_0^{x_f} |\Psi_N (x)|^2 \, dx }}$

What is the probability of detecting the particle in the region $( 0 \leq x \leq 1)$ ? If the probability is $P$ , give your answer as $\lfloor 100 P \rfloor$ .

Note: This problem lends itself well to numerical solution