Quantum Well - Squared Cosine Potential
A particle in a one-dimensional quantum well is governed by a variant of the time-independent Schrodinger equation, expressed in terms of wave function Ψ ( x ) .
The quantities V and E are the potential energy and total energy, respectively.
− d x 2 d 2 Ψ ( x ) + V ( x ) Ψ ( x ) = E Ψ ( x )
The potential varies as follows:
V ( x ) = ∞ x < − π V ( x ) = cos 2 x − π ≤ x ≤ π V ( x ) = ∞ x > π
The boundary conditions on Ψ ( x ) are:
Ψ ( x ) = 0 x ≤ − π Ψ ( x ) = 0 x ≥ π
Let E 1 , E 2 , and E 3 be the lowest, second lowest, and third lowest allowable values of E , subject to the constraint E > 0 . Determine the following ratio:
E 2 − E 1 E 3 − E 2
Note: Only apply the Schrodinger equation within the finite potential region
The answer is 2.87.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I used the same procedure outlined by @Karan Chatrath . What we want to do is make a graph of E vs. the value of Ψ at the right end of the well, assuming that we initialize properly at the left end of the well for each value of E . The allowable values of E are those for which the graph crosses the horizontal axis. The code for making the graph is attached.
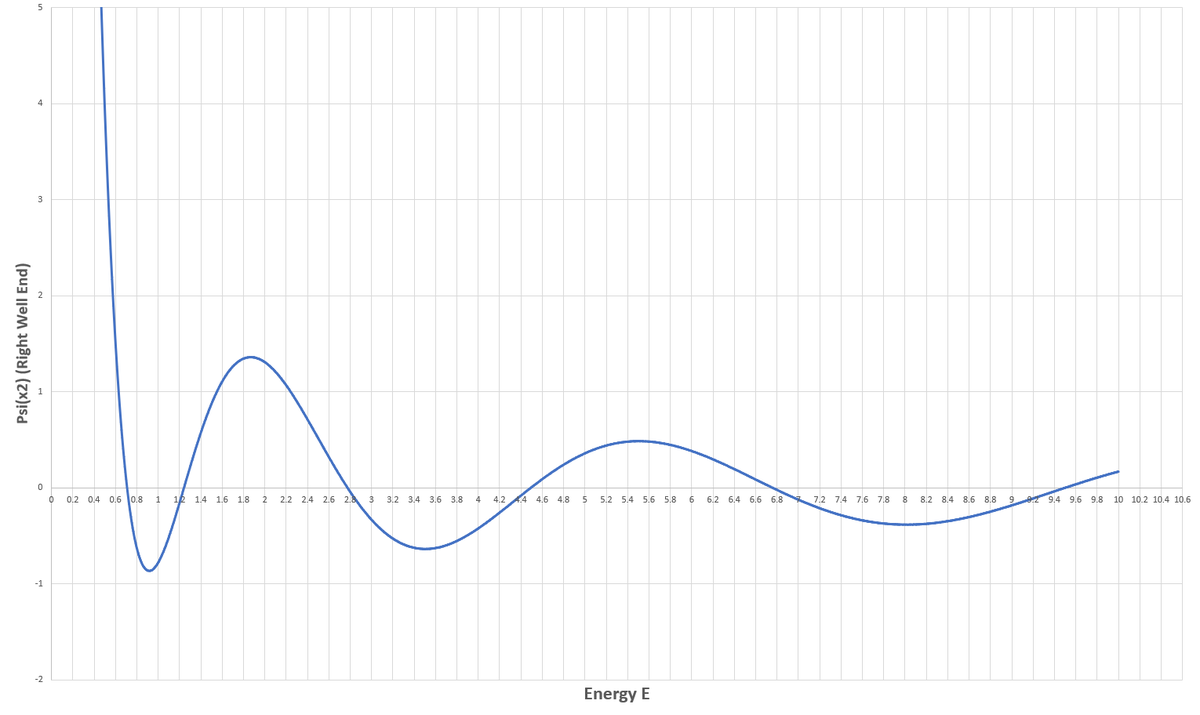
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
|
Very nice! From the looks of the plot, the gap between successive allowable energies increases as energy increases.
Log in to reply
Indeed. I was thinking back to the simple potential-free textbook quantum well. And the energy there is proportional to n 2 , where n = 1 , 2 , 3 , e t c . . The gaps between energy levels increase there too, as a result of the n 2 dependence. Just for fun, I ran this same code with V = 0 and reproduced the results for the classic quantum well, showing the n 2 dependence. The ratio in that case is 4 − 1 9 − 4 = 3 5 .
Log in to reply
Interesting. Running the V = 0 case is a good way of cross-checking one's code cause the results are well known. I say this especially since in the last problem, my code had some errors.
This problem was treated purely numerically. Steps performed are as follows:
A plot showing the wave functions at different allowable energy levels is as follows: