Quantum Well with Exponential Potential

Classical Mechanics Level 5

A particle in a one-dimensional quantum well is governed by a variant of the time-independent Schrodinger equation, expressed in terms of wave function $\Psi (x)$ .

The quantities $V$ and $E$ are the potential energy and total energy, respectively. $E$ is a positive constant.

$-\frac{d^2}{d x^2} \, \Psi (x) + V(x) \, \Psi (x) = E \, \Psi (x)$

The potential energy varies as follows (where $e$ is Euler's number):

$V(x)= \begin{cases} \infty, &\,\, x < -3 \\ e^x, &\,\, -3 \leq x \leq +3\\ \infty, &\,\, x > +3 \\ \end{cases}$

The boundary conditions on $\Psi (x)$ are:

$\Psi(x) = \begin{cases} 0, \,\, x \leq -3 \\ 0, \,\, x \geq +3 \\ \end{cases}$

For the smallest allowable $E$ such that $E>0$ , what is the probability of detecting the particle in the region $x > 0$ ?

Bonus: Make a plot of $\Psi^2(x)$ . Does this result agree with intuition derived from classical mechanics?

The answer is 0.0793.

2 solutions

Karan Chatrath
Feb 2, 2021

The result agrees with the intuition derived from classical mechanics. In classical mechanics, a particle finds its point of stable equilibrium which corresponds to minimum potential energy. In quantum mechanics, the analogous argument is that the particle is more likely to be found in the inverval where potential is lower. Attached below is commented code:

clear all, clc

% Spatial discretization:
dx      = 1e-4;      x       = -3:dx:3;

% Allowable Energy:
E = 0.996400995;

% Left boundary condition:
psi(1)  = 0;         dpsi(1) = 1;


% Numerical integration
for k = 1:length(x)-1

  ddpsi      = (exp(x(k)) - E)*psi(k);

  % Semi implicit Euler:
  dpsi(k+1)  = dpsi(k) + ddpsi*dx;
  psi(k+1)   = psi(k) + dpsi(k+1)*dx;

end

% A1 is area when x>0 and A2 is total area initialisation:
A1 = 0;      A2 = 0;

% Area computation using Explicit Euler:
for k = 1:length(x)

  if x(k) > 0
    A1 = A1 + psi(k)^2*dx;
  end

  A2 = A2 + psi(k)^2*dx;

end

% Probability of particle lying in x>0:
P = A1/A2
% P = 0.079233

Thanks for the solution. I have added a few more plots since the initial posting

Steven Chase - 4 months, 1 week ago

How did you find the lowest allowable energy to be 0.9964...?

Veselin Dimov - 4 months, 1 week ago

I did it by trial and error. I used the boundary condition at $x=-3$ and assigned an arbitrary value for the derivative of $\Psi$ at that point. I then tuned the value of $E$ till the second boundary condition ( $\lvert\Psi(3) \rvert \le \epsilon$ ) was satisfied, where $\epsilon$ is a very small number like $10^{-4}$ , for example.

Karan Chatrath - 4 months, 1 week ago

Steven Chase
Feb 2, 2021

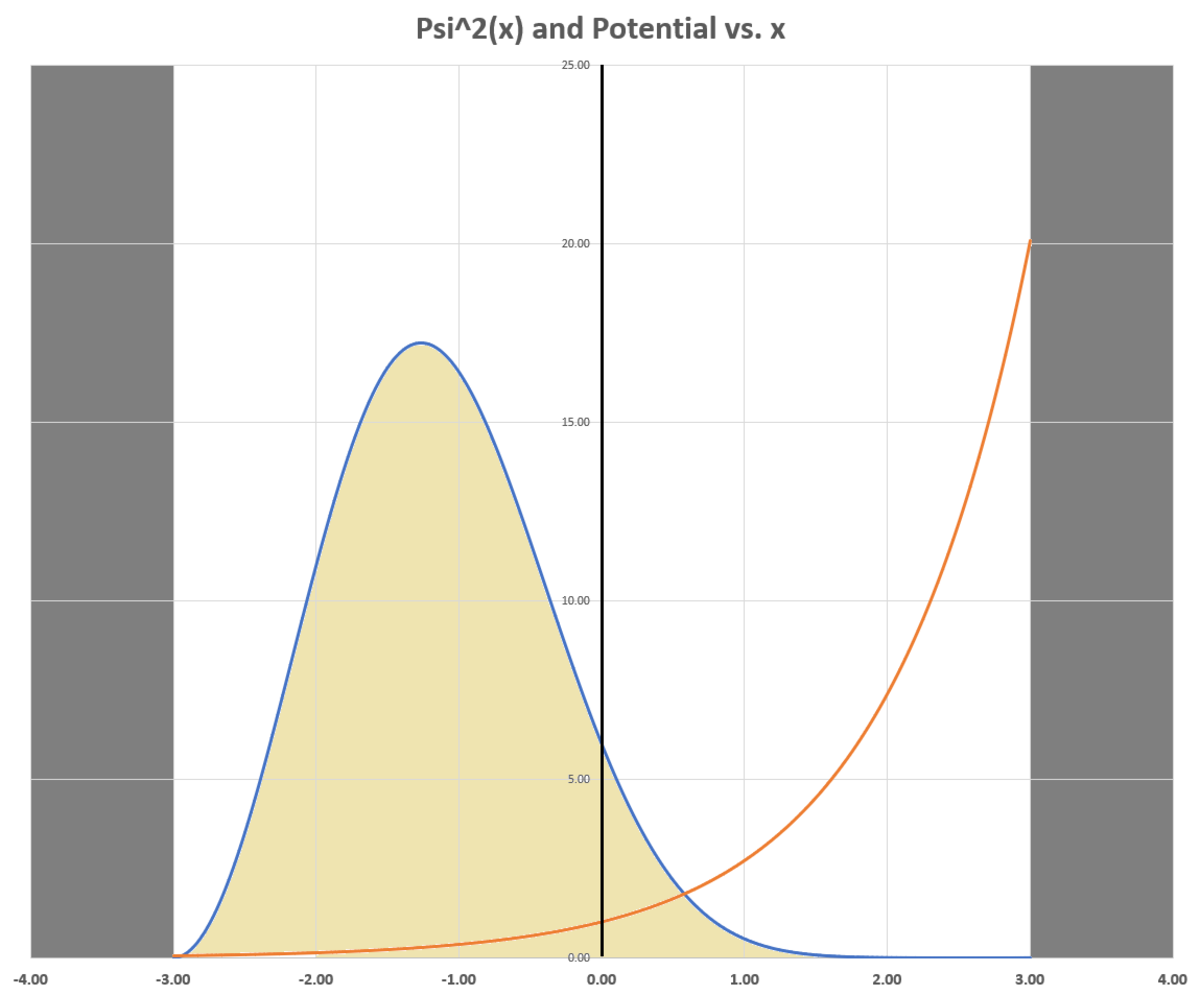
Here is an illustration of $\Psi^2(x)$ and the potential function $e^x$ within the well (wave function is not normalized). The area under the $\Psi^2(x)$ curve is shaded in tan color, since the probabilities are related to this area. The probability of finding the particle in the region $x > 0$ is the tan area in the $x > 0$ region divided by the total tan area. As observed by @Karan Chatrath, the particle "prefers" the low potential region in while in the lowest energy mode, which is analogous to classical behavior.

I have also included plots for the second, third, and eighth lowest energies (modes 2, 3, and 8). You can see that the number of humps in the $\Psi^2(x)$ plot matches the mode number. There is still an aversion to the high potential region, but it is less pronounced at higher energies.

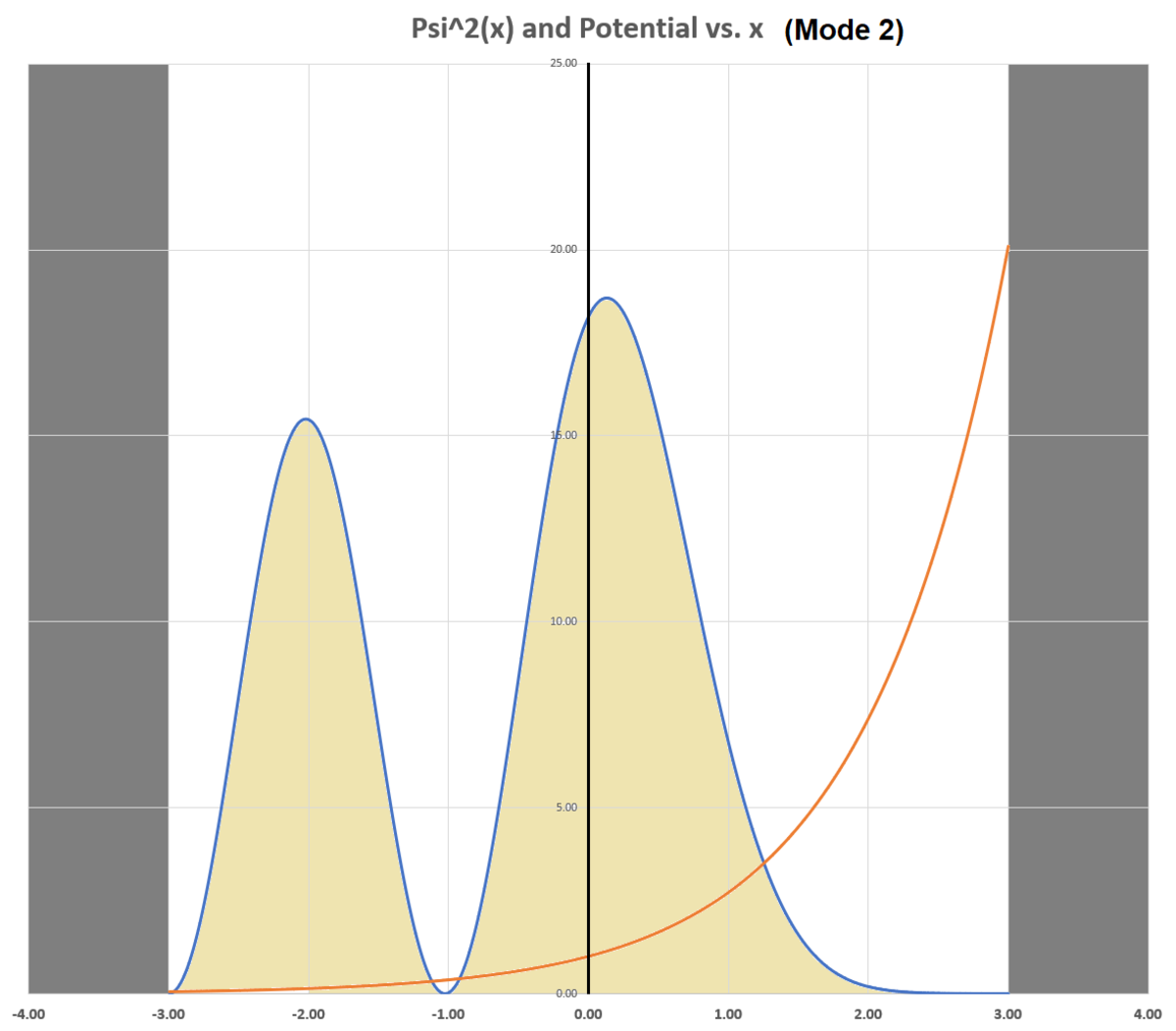
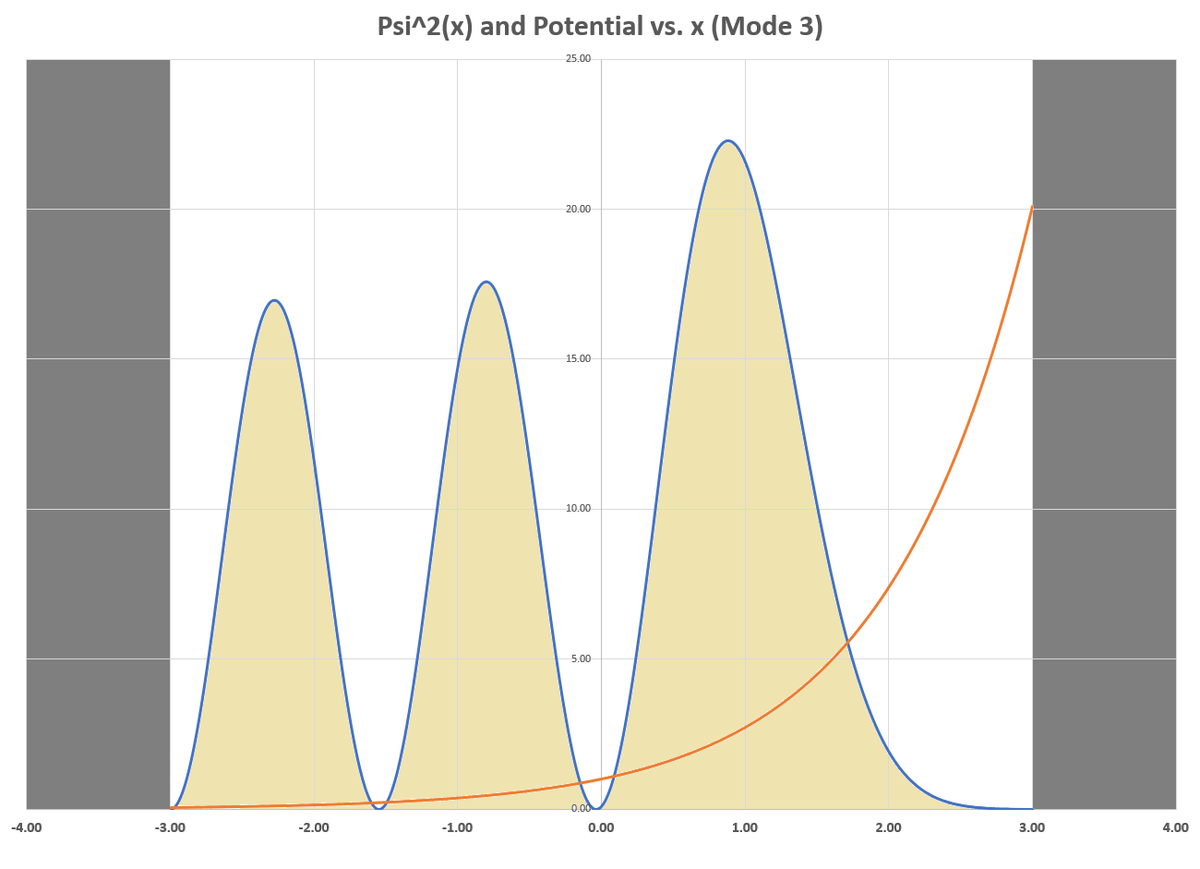
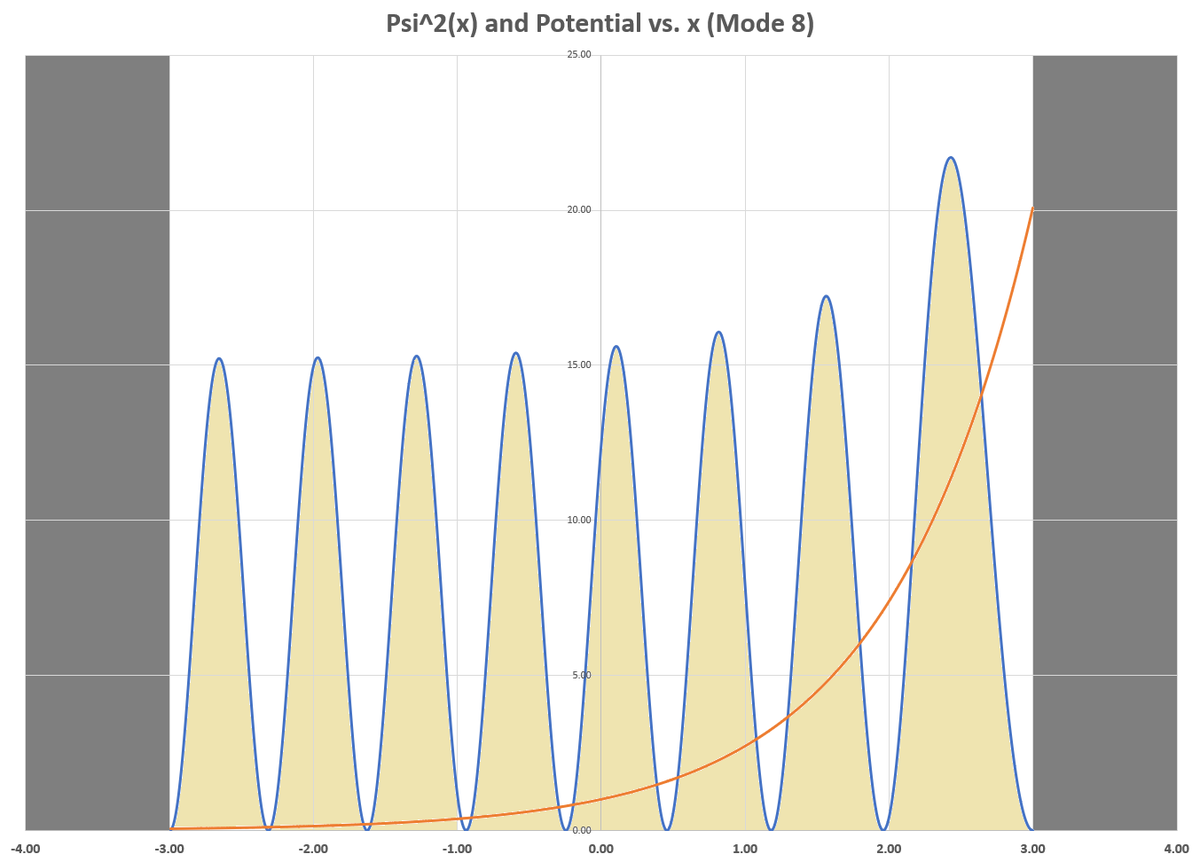
So at lower energies, one can expect better agreement with classical thought? Is that a valid conclusion?

Karan Chatrath - 4 months, 1 week ago

My interpretation is that high energy particles can sort of disregard the inner potential and go wherever they want, whereas low energy particles have to respect the potential distribution more

Steven Chase - 4 months, 1 week ago

You could take a bucket and put some ridges or ripples inside on the bottom and put a marble in. At low energies, the marble would be trapped between two ridges. At high energies, the marble could traverse the whole inside of the bucket and disregard the ridges somewhat.

Steven Chase - 4 months, 1 week ago

Helpful analogy, thanks for this

Karan Chatrath - 4 months, 1 week ago

Interpretation-wise, you are missing the point. Consider the following plots, showing the first 9 energy levels and their (scaled for visibility) associated states. I have also plotted the energy level against the potential.

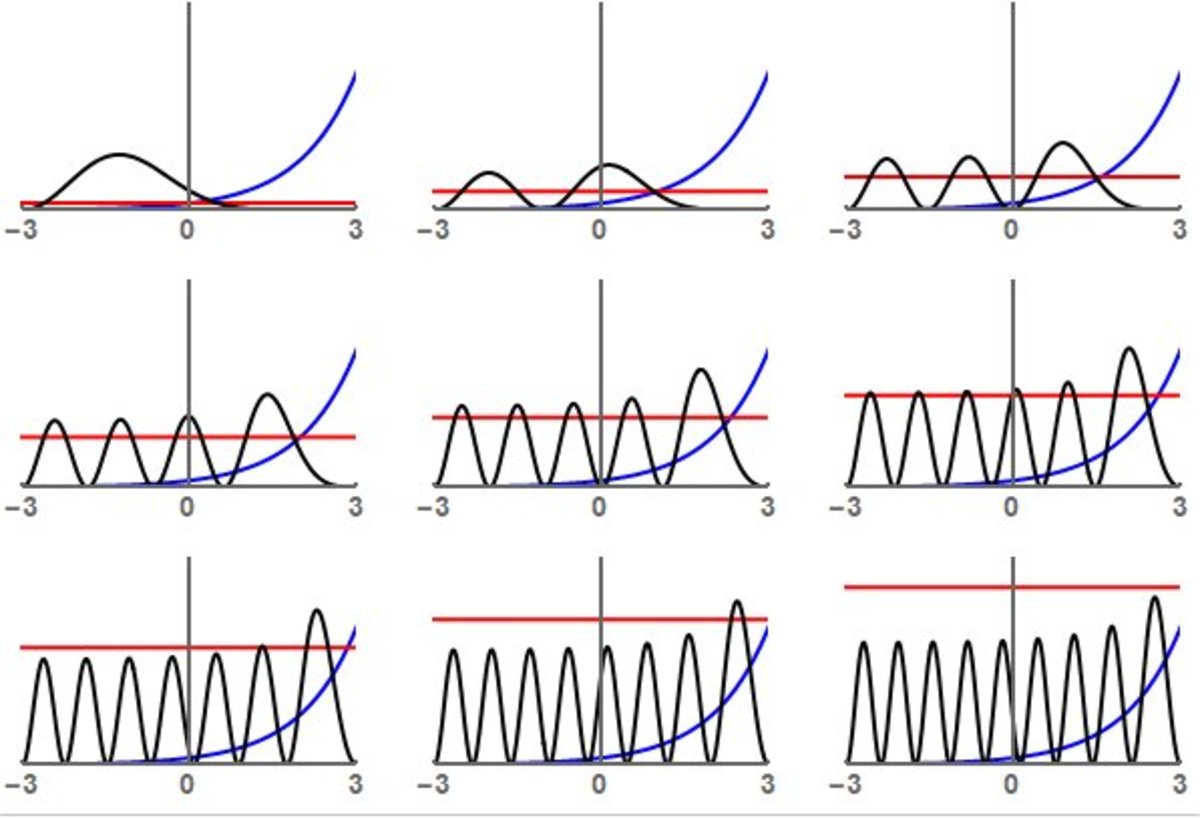
In regions where the potential is smaller than the energy level, ordinary oscillatory wave functions occur. Classically, there is no problem with the particle occurring in that region. However, in the regions where the energy level is less than the potential (classically, the particle should not be there) there is a degree of quantum tunnelling, which eventually peters out - periodic wave functions do not occur in these regions.

After the first 9 energy levels, the energy level is greater than the potential throughout $-3 \le x \le 3$ , so there is no classical obstruction, and no need for quantum tunnelling.

Mark Hennings - 4 months, 1 week ago

Thanks for the insights. Naively, we could say that $E$ is the sum of the kinetic and potential energies:

$E = T + V$

In the quantum tunneling region, $V > E$ and $T$ is correspondingly negative. What do we make of that negative kinetic energy value? Maybe we just think of $E$ as an eigenvalue associated with the Hamiltonian, rather than trying to equate it to a sum of kinetic and potential energies?

Steven Chase - 4 months, 1 week ago

You are still thinking too classically. Imagine a beam of electrons of energy E approaching a finite square well potential of width $a$ and height $V_0 > E$ . Classically, there would be total reflection. This does not occur in QM. Electrons still have a chance of penetrating a region of higher potential, although that chance decreases with $V_0$ and $a$ , so there is still a chance that some electrons will make it through a finite barrier.

Try solving $-y'' + Vy = Ey$ where $V=0$ for $x<0$ and $x>a$ and $V=V_0$ for $0<x<a$ . If we have $y=e^{ikx} + Ae^{-ikx}$ for $x < 0$ representing a beam of electrons of fixed energy iincident from the left, and a beam of reflected electrons, there will be a nonzero solution $Be^{ikx}$ for $x > a$ , representing the proportion of electrons that tunnel through the "impenetrable" barrier.

If the barrier $V_0$ was semi-infinite, so $V = V_0$ for $x > 0$ , then the solution to the right of the origin would be of the form $e^{-\kappa x}$ , where $\kappa = \sqrt{V_0-E}$ . There would be some penetration, but not through current. Indeed, in this case $|A| = 1$ , which would indicate total reflection.

Mark Hennings - 4 months, 1 week ago

Quantum Well with Exponential Potential

The answer is 0.0793.

2 solutions

0 pending reports