Quarter Point Geometry
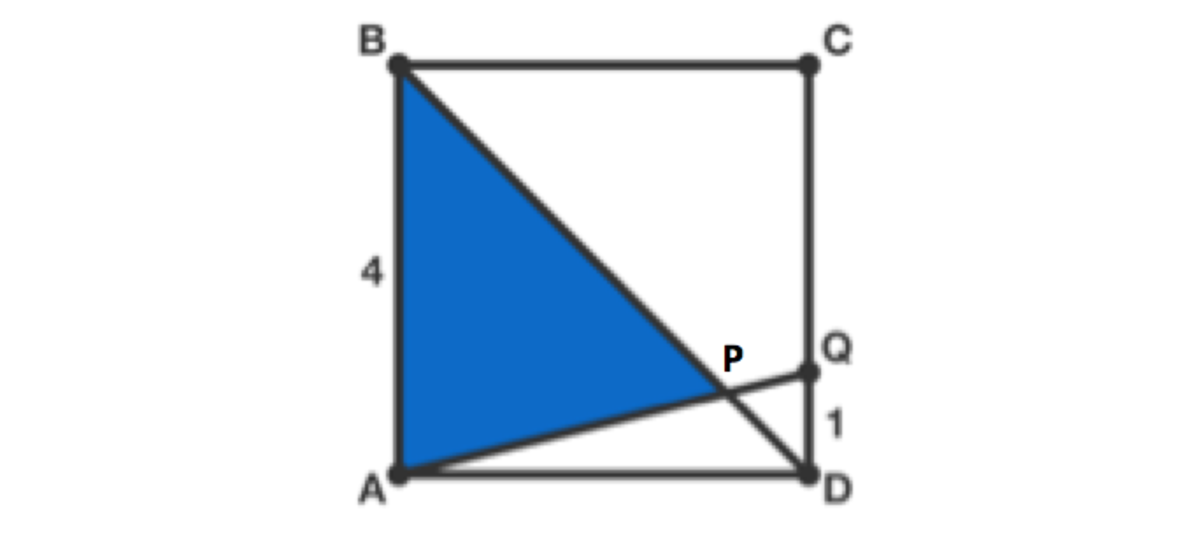
What percentage of the square's area is colored blue?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
25 solutions
RE: The triangles containing areas x and z are similar, with a ratio of 4:1, so the ratio of the areas is 16:1 This would be better clarifying if said as triangles x and z, as similar, have corresponding SIDES whose ratios are 4:1, so their areas have a ratio of 16:1 (when I first read it, it threw me, esp. as the areas define the shapes of the two triangles, thus it would seem if the ratio of triangles x and z are 4:1, then their areas should also be 4:1)
We were asked for a simple solution - a 'trick'. This is my logical solution with a minimum of mathematics. The area of BCD is 8 or 50% of the area of ABCD. The area of AQD is 2 or 12.5%. The total area of these 2 triangles is 10/16 or 62.5%. As they overlap by a small amount, the blue area is a little more than 37.5%. The overlap area is less than 1 or 6.25%. So the blue area is no more than 37.5% + 6.25% or 43.75%. So the only possible answer on the list is 40%.
Log in to reply
Nice solution. I prefer not to use the multiple choice answers as part of answering the question, but that is a matter of taste, I agree.
The blue triangle is similar to the small white triangle on the right, but 4 times larger. Thus the triangles together divide the width of the square in a 4:1 ratio, or 80%:20%.
The vertical extent of the blue triangle ("base") is 100%. The horizontal extent ("height") is 80%. Thus the area is 2 1 ⋅ 1 0 0 % ⋅ 8 0 % = 4 0 % .
Got it! Interesting perspective. The only thing that sounded strange was "the blue triangle is 4 times larger". It's actually 16 times larger, but I think you were talking about the edge length.
Log in to reply
Its area is indeed 4 2 times larger. When comparing similar figures, it is customary to give their linear ratio; but I could have been more specific.
You are right. The ratio of the widths of the two similar triangles is 4:1. The area of the blue triangle (base x width / 2) is 4 x (4 x 4/5) x 1/2 = 32/5. The area of the square is 16. So the ratio of the area of the blue triangle to the square is 32/5 : 16 or 2/5 : 1 or 40% of the square.
Very elegant. I like it.
The blue triangle and the small triangle are similar. Their corresponding bases are in the ratio of 4/1,so their areas are in the ratio of 16/1. Let the areas be 16x and x .Now,let the blue triangle be named 'a',the right triangle below it be named 'b' and the small triangle be named 'c'. ar(a+b)=8 , ar(c+b)=2. Then,ar(a-c)=6. 16x-x=6 or 15x=6. x=2/5. ar(a)=(16) (2/5)=3.2 area of the square =(4) (4)=16 so the blue triangle covers(3.2/16)*100=40% of the area of the square
Both lines AD and BC can be seen as linear lines: y = 0.25x and y = 1 - x. These lines intersect at x = 0.8. So the blue area = 0 . 5 × 1 × 0 . 8 = 0 . 4
That was a short way to go. What's going on in the last equation?
Log in to reply
I considered the square to be 1 unit by unit, so the last equation is a triangle with base 1 and hight 0.8. If I used the normal length of 4, the blue area would be 6.4 and the square 16. Which gives a extra calculation toe get to 40 %.
Well, if the intercept point is 16/5 (which is 0.8), then the height of the blue triangle is 16/5 if you consider the base to be 4. Then it's just area of a triangle = 1/2 x base x height.
It's actually the same thing Arjen did. Notice the parallel: 1/2 * 100% * 80% vs 0.5 * 1 * 0.8 They used the same method, only differing in how they found the "horizontal extent" of the blue triangle.
...after rescaling. Which isn't to say your solution is incorrect. The percentage will stay the same after rescaling. But the equations might throw people off if they're looking for y = 4 - x instead of y = 1 - x.
Log in to reply
I should point out this answer was posted to the original problem (which was on a unit square). It was tweaked for POTW for simplicity of presentation.
You mean AQ and BD?
Area of square = 4 x 4 = 16 Area BCD = 8, Area AQD = 2, Area BCD + AQD = 10 Area of Z: 0 < AreaZ < 1, since a triangle not a cube of 1 x 1. Area of white space ranges from 10-1 to 10-0. i.e: 9 < areaWhite < 10. Therefore Area of Blue Area ranges from 16-9 to 16-10: i.e: 6 < areaBlue< 7 % ranges from 6/16 to 7/16 or 0.375 to 0.4372. Only answer in that range is 40%. Not exact but only mental math needed
Let S be the point of intersection of BD and AQ. Then BDA is 1/2 of the whole, ADQ is 1/8, and QDS is unknown x. Blue area is 3/8+x, and x is (3/8+x)/16 by similarity. By infinitely substituting x and solving infinite geometric sequence we get the blue area of 2/5.
Let “P” be the point where the interior lines intersect. By similar triangles, BAP (the blue area) = 16 PDQ. By equal altitudes, PAD = 4 PDQ. Half the square is BAP + PAD = 20 PDQ. The whole thing is 40 PDQ. 16 PDQ/40 PDQ = 2/5 = 40%
With A being O(x,y)
R B D : y = − x + 4
R A Q : y = 4 1 x
R B D = R A Q ⇒ x = 5 1 6
Blue Area equal ( 4 ∗ 5 1 6 ) / 2 , Total area is 4*4=16 so Blue/Total = 5 2 = 0 . 4 = 40%
Much better solutions above than mine. My hard way was
let M be the intersection of AQ and BD
Then 2 1 x A Q A M gives the answer.
if angle QAD = α
Then AMD = 180-45-α and sin(AMD) = sin(45+α) = sin45 cosα + cos45 sineα
sinα = s q r t ( 1 7 ) 1 , cosα = s q r t ( 1 7 ) 4
Then sine rule gives us s i n α A M = s i n ( A M D ) 4
And all the surds end up simplifying to 5 2 and 40%
I used similar triangles and got 40% but my hand brushed the wrong answer. Grrr!
The whole side of that diagonal since it forms a triangle has an area of 8. The small side gives an area of 2. Which means the other side of the diagonal is 6 in area. By ratio 1 in area is 6.25 in percent hence 6 is 37.5in percent . Get the full bottom area which is white and you get 12.5 in percent then subtract the 2.5 in percent for the smallest side from it to get 10 percent. Subtract from 50 which is the percentage of the full diagonaland you get 40 percent.
We can find all three angles of the shaded area, and because we have one of the side lengths, we can use the law of sines to calculate the other two sides. Then we can use Heron's Law to find the area. We'll define the point of intersection as G. Now angle ABG is 45 degrees. Angle DAQ is atan 1/4 (because tan DAQ is opposite/adjacent is 1/4). So angle BAG is 90 - atan 1/4. Finally, since all the angles of a triangle add up to 180, angle AGB is 45 + atan 1/4.
Now we can use the law of sines. sin 5 9 . 0 3 6 2 4 3 4 = sin 7 5 . 9 6 3 7 5 6 B G = sin 4 5 A G which resolves to BA = 4, BG = 4.525483, and AG = 3.298484. Heron's formula is p ( p − a ) ( p − b ) ( p − c ) where p is the semiperimeter, or half the perimeter, or 5.911984. The area is approximately 6.4 by this formula. 6.4/16 = 0.4, where 16 is the area of the square. Thus the shaded triangle is 40% of the square.
Maybe this is considered too long a path to an answer, but my reasoning is:
Let the intersection of BD and AQ be vertex P and observe that we have AAS similarity between triangle ABP and QDP.
Given that ABCD is a square we have with the Pythagorean theorem that BD = 4 2 and since BP:DP :: 4:1 we have BP = 5 4 * 4 2 = 5 1 6 * 2 .
Now, angle ABD = angle ABP = 45° since, by construction, angle ABD is the angle bisector of angle ABC which is 90°. P is on BD so angle ABD = angle ABP.
Using the area formula 2 ( A B ) ( B P ) s i n ( A B P ) and knowing that angle ABP = 45° so sin(ABP) = 2 1 we can compute that the area [ABP] = 2 1 (4 * 5 1 6 * 2 * 2 1 ) = 5 3 2 .
This means that [ A B C D ] [ A B P ] = 1 6 3 2 / 5 = 8 0 3 2 = 5 2 .
In other words: The area of triangle ABP = 5 2 * [ABCD] = 40% of the area of the square.
Similar triangles so 4/1 = ab/qd =l / n Let l be the height for for bigger triangle and n be the height for smaller triangle. l+n =4, l=4n, 4n +n =4; n=4/5; l = 16/5; area of shaded = (4 16/5)/2=6.4 square units Area of box= 4 4=16 (6.4/16)*100% =40%
A B and D Q are line segments which are the sides of two similar triangles intersecting at unmarked vertex P . If Q and D are equal, then the area of the triangle △ A B D would be 2 1 the area of the square A B C D . Similarly if Q and C are equal, then the area of triangle △ A B P and triangle △ Q D P would also be 2 1 the area of the square. The sum of the areas of triangle △ A B P and triangle △ Q D P must always be constant at 2 1 the total area of the square A B C D . In fact, you can extend this further by saying that Q is the point of intersection of a line A R which has an angle ∠ B A Q which ranges from 0 ∘ to 9 0 ∘ . As similar triangles, the height h of triangle △ A B P and triangle △ Q D P must therefore be proportional to each other by the ratio of the lengths of line segment A B to line segment D Q . At 4 : 1 the area of triangle △ A B P = ( 2 1 ) ( 1 + 4 4 ) = 4 0 % .
let x be the smallest part in picture, (x/6+x) = (1/16), x= 6/15 Therefore 6+6/15 = 6.4 and 6.4/16 = 0.4
I am a mechanical engineer and know how to caculate this but... You dont have to calculate. Just know half of the square is 50%. This is under 50%. Cannot be 30% becasuse that’s too small. Would be less than 1/3 of the square. For similar reasons 45 and 35 are discarted. Only 40 is left as a logical answer. Additional information: You have to take into account the possible solutions instead of doing all the math and then see if it matches one of the possible answers. We often ignore our observation and jujement capabilities and embark in complicated calculations to get to something we already knew. This is out of the box thinking.
Blue and Smaller White ∆s are similar. Hence all of their sides and height will be in same ratio, i.e. 4:1. Sum of the heights of these ∆s is 4(side of square). Therefore the height of blue∆ = 16/5. Area = 32/5 , hence 40%.
You do not really need writing for this question, mental arithmetic is already enough.
The two triangles inside of the square are similar, given the ratio of the two parallel sides is 4:1, so their heights' ratio is also 4:1.
Therefore, the blue triangle's height is FOUR FIFTH the side length of the whole square.
Area of the whole square = 4 * 4
Area of the blue triangle = 4 * (1/2) * 4 * (4/5)
The proportion is easy to see, it is just the product of two extra factors, which makes 40%.
Nice, easy, simple method: 4/5 * 50. 40.
BOOM! MIND BLOWWWWWN
 .
.
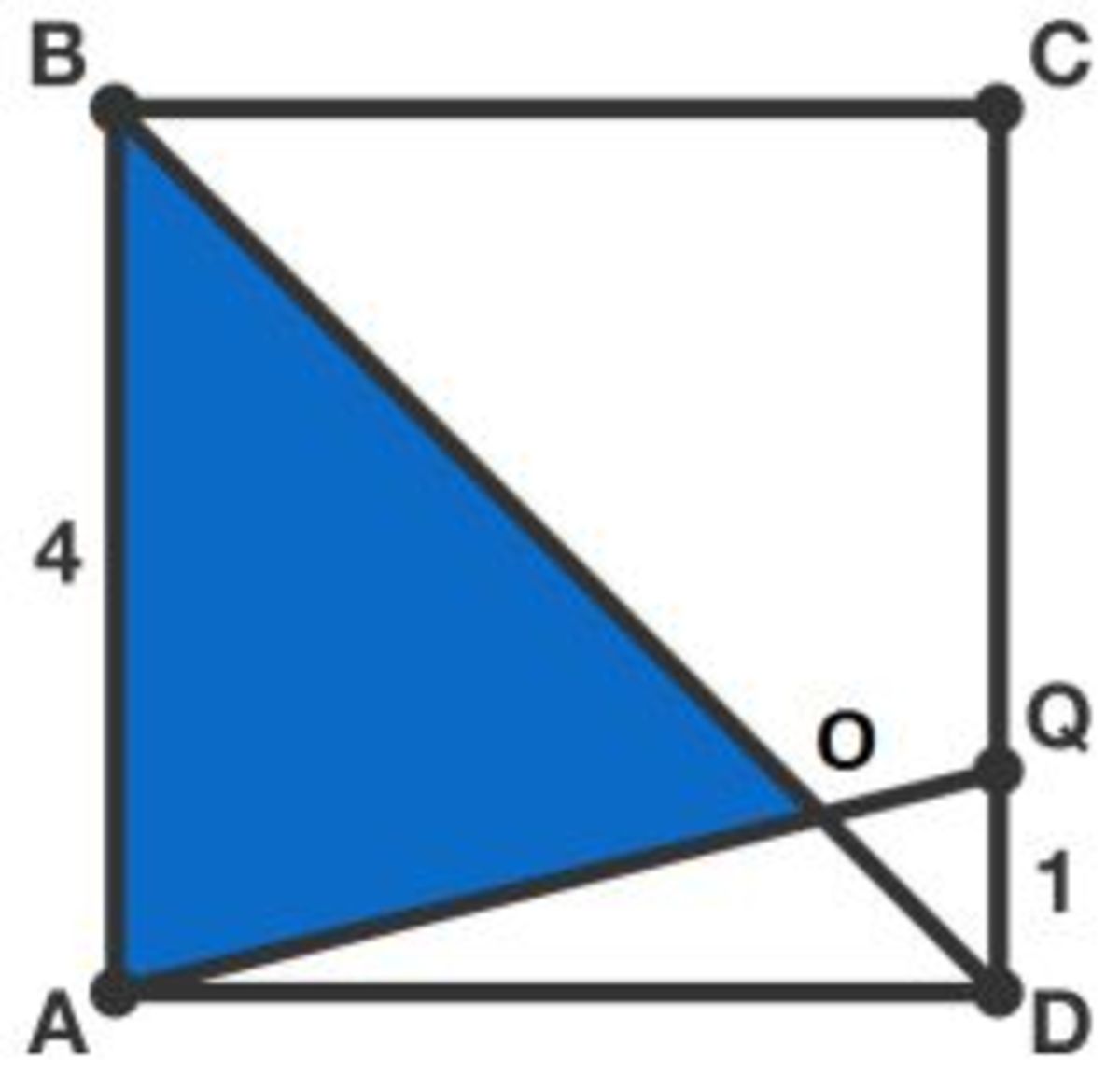
Let's call X the area of triangle ABO. The area or triangle DQO will then be X/4. Adding them, we'll get half of the square area. That is, X + X/4 = 8 => X = 32/5.
So, the ratio of X (blue triangle ABO) to the square = (32/5)/16 = 40%
The heights of the two triangles wedged between AQ and BD are in the ratio 4:1. Hence the height of the bigger triangle is 4/5 times the length, 4.
Area of shaded triangle = 1/2 × 4 × 3.2 = 6.4
Area of square = 4 × 4 = 16
6.4/16 = 40%
Call K the point of intersection of BD and QA. The altitude of triangle ADK from K to AD is half the harmonic mean of 4 and 1, which is 4/5. Thus [ADK]=(4/5)(1/2)(4)=8/5. Furthermore, [BDA]=(1/2)(4)(4)=8, and since [BKA]=[BDA]-[ADK]=8-8/5=32/5, the percentage of the square colored blue is (32/5)/16=2/5=40%
Flip Y about the BD axis to show it is four times the size of the small triangle Z - same height with bases in ratio 1:4
Y + Z = 2, so Y is 1.6 or 10% of the square, therefore the blue area is 50% - 10% = 40%
Let B D and A Q intersect at point P .
Let ∠ D A P = θ ⟹ ∠ B A P = 9 0 − θ and ∠ A B D = 4 5 ∘ ⟹ ∠ B P A = 4 5 + θ ⟹ ∠ Q P D = 4 5 + θ and ∠ C D P = 4 5 ∘ ⟹ ∠ D Q P = 9 0 − θ
∴ △ A B P ~ △ D P Q
Let the height of △ A B P = x ⟹ the height of △ D P Q = 4 − x ⟹ 1 4 = 4 − x x ⟹ x = 5 1 6 ⟹
A △ A B P = 5 3 2 ⟹ 5 3 2 = 1 0 0 x ∗ ∗ 1 6 ⟹ x ∗ = 4 0 %.
Let O be the point in which lines BD and AQ intersect. Note that angles BOA and QOA are equal, because they're opposite by a vertex. Furthermore, angles ODQ and OBA are also the same, (because lines AB and DC are parallel, and they're cut by line BD, so the angles in the same region but different semiplane must ve equal). This means that triangles AOB and DOQ are similar triangles. And because AB is 4 times longer than DQ, sidelenghts of triangle AOB are 4 times longer than sidelenghts of triangle DOQ, which means the area of triangle AOB is 16 (4^2) times the area of triangle DOQ. Let x be the area of DOQ. We can work out that the area of BCD is 8 and that the area of AQD is 2. So we have that: 16x + (8-x) + 2=16 (we substract x because of the overlapping of triangles BDC and AQD). Solving for x gives that Ar(DOQ)= 2/5, and Ar(AOB)= 32/5. Finally, we do (32/5)/16= 0.4= 40%.
New Solution: 8 times the area of Triangle QAD = the area of Square ABCD. * / / / Area of Triangle OQD ~ (1/4) area of Triangle QAD (by eyeballing). Triangle ABD = 1/2 the area of the square. Area of the blue Triangle ABO = area of Triangle ABD minus the area of Triangle ADO. ** So, the area of Triangle QAD = (1/8) times the area of Square ABCD.
The percent of the area ~ (1/2) - [1/8 - (1/4)(1/8)] = (1/2) - [1/8 - 1/32] = (1/2) - [4/32 - 1/32] = (1/2) - [3/32] = (16/32) - (3/32) = 13/32 = 39/96 ~ 40/100 = 40%
(a) x + y = 50% (half of the square)
(b) y + z = 12.5% (half base x height)
The triangles containing areas x and z are similar, with sides with a ratio of 4:1, so the ratio of the areas is 16:1
(c) x = 16 z
From here its an easy simultaneous equation:
Substituting (c) into (a) gives
(d) 16 z + y = 50%
Subtracting (b) from (d) gives
15 z = 37.5%
=> z = 2.5%
=> x = 40%