Quartic Query
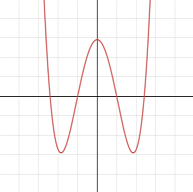
A quartic equation has real zeros ± p and ± q so that its 3 horizontal tangent points are equidistant to the x -axis.
If p > q > 0 , the ratio q p can be expressed as a + b , where a and b are integers.
Find a + b .
The answer is 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Great solution!
We have f ( x ) = ( x − p ) ( x + p ) ( x − q ) ( x + q ) = x 4 − ( p 2 + q 2 ) x 2 + p 2 q 2 = ( x 2 − 2 p 2 + q 2 ) 2 + p 2 q 2 − 4 ( p 2 + q 2 ) 2 , with a minimal value of p 2 q 2 − 4 ( p 2 + q 2 ) 2 when x = ± 2 p 2 + q 2 . We want this minimal value to be − f ( 0 ) = − p 2 q 2 . The equation p 2 q 2 − 4 ( p 2 + q 2 ) 2 = − p 2 q 2 simplifies to 4 p 2 q 2 = ( p 2 − q 2 ) 2 and 2 p q = p 2 − q 2 . Solving this quadratic equation for p gives p = ( 1 ± 2 ) q . Since it is required that p > q we have q p = 2 + 1 and the answer is 3 .
This is a great solution!
Let f ( x ) = ( x 2 − p 2 ) ( x 2 − q 2 )
Distance of horizontal tangents from x-axis = |Value of function at that point|.
∴ , f ( 0 ) = ∣ f ( c ) ∣ , for which f ′ ( c ) = 0 (c≠0)
The derivative of this function becomes zero at x = 0 , ± 2 p 2 + q 2 .
Putting in the values, we get,
f ( 0 ) = p 2 q 2
f ( c ) = − ( 2 p 2 − q 2 ) 2
Equating them both, and putting q p as y , we get a quadratic equation,
y 2 − 2 y − 1 = 0 , whose solution is y = 1 ± 2 . (Only the positive solution is taken as both p and q are >0).
The equation being described is f ( x ) = ( x − p ) ( x + p ) ( x − q ) ( x + q ) = x 4 − ( p 2 + q 2 ) x 2 + p 2 q 2 We want to know the locations of the local extrema, so we take the derivative of this function, and set equal to zero: 0 = 4 x 3 − 2 ( p 2 + q 2 ) x From this equation and the symmetry of the quartic, zero is clearly an extreme. Dividing out an x leaves a simple quadratic with roots of ± ( p 2 + q 2 ) / 2
Next, plug in these values to get the actual heights. After simplifying, 0 gives p 2 q 2 and ( p 2 + q 2 ) / 2 gives − ( p 2 + q 2 ) 2 / 4 + p 2 q 2 . Set one height equal to the negative of the other (to account for sign), and you’re done! Well, mostly.
We have an equation relating p and q, now we just need to transform it into a ratio between them. If you’re lazy like me, plug it into a grapher, and you’ll see 4 lines through the origin; the slope of the line where p>q>0 is the answer. But we’ve come this far without a calculator, let’s finish without one.
First, make the replacements P = p 2 and Q = q 2 . Then, rearrange our equality to get 0 = P 2 − 6 P Q + Q 2 Treat P as the variable and Q as a constant. Plug into the quadratic formula, and get P = 3 Q + 2 2 Q .
P/Q is then 3 + 2 2 . P/Q also happens to be ( p / q ) 2 . Since 3 + 2 2 = 2 + 2 2 + 1 = ( 2 + 1 ) 2 our answer is 2 + 1 = 3