Queen's Domain
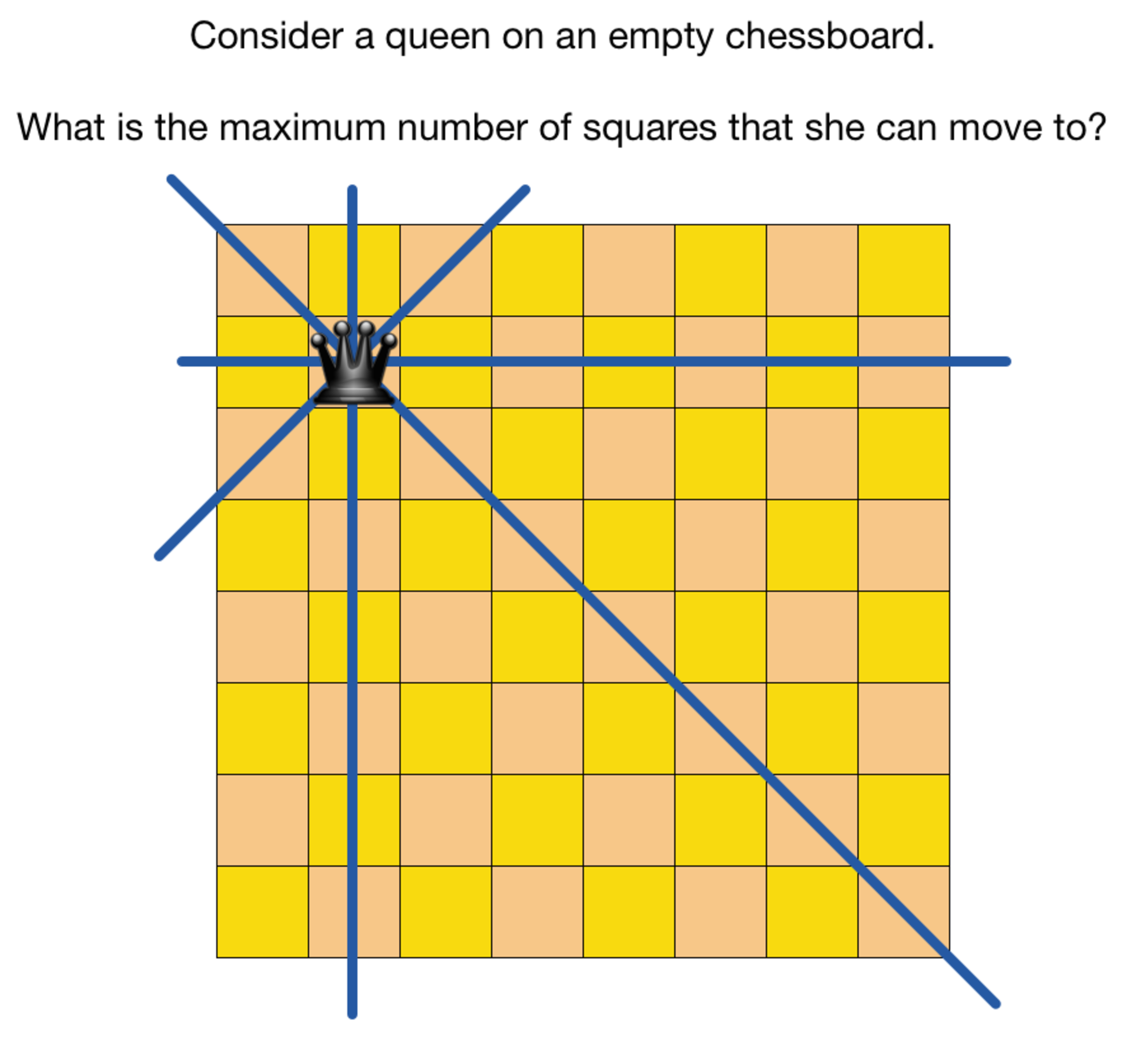
A queen stands on an otherwise empty standard ( ) chessboard.
What is the maximum number of squares that are accessible to the queen in a single valid move?
Assumption :
Standing still does not count as a move.
The answer is 27.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Relevant wiki: Chess Puzzles
The number of "rook-like " moves that the queen can make , starting from any square, is always 1 4 , so it suffices to maximise the number of "bishop-like" moves. Note that the "rook-like" and "bishop-like" moves are mutually exclusive and exhaustive.
Note that a diagonal in a chessboard can have at most 8 squares, and at most 7 other squares that a queen can access if she is already on that diagonal. So there can be at most 7 + 7 = 1 4 "bishop-like" moves she can make. But equality can't hold, because the two longest diagonals are oppositely coloured. So no more than 1 3 such moves can be made. Equality can clearly hold when the queen stands on some central square.
The answer is 1 4 + 1 3 = 2 7 .