Ques. -20

Geometry Level 4

Given the four lines with the equations ( x + 2 y − 3 = 0 ) (x+2y-3=0) , ( 3 x + 4 y − 7 = 0 ) (3x+4y-7=0) , ( 2 x + 3 y − 4 = 0 ) (2x+3y-4=0) , ( 4 x + 5 y − 6 = 0 ) (4x+5y-6=0) , then :

If you're looking to promote your Rank in JEE-MAINS-2015, then go for solving this set : Expected JEE-MAINS-2015 .
They are all concurrent. They form a cyclic quadrilateral. They are the sides of a non-cyclic quadrilateral. None of the given is true.

View wiki
Sandeep Bhardwaj by Sandeep Bhardwaj , 28, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Thomas Lee
May 30, 2015

I personally like to rewrite the equations into y = m x + b y=mx+b and when you do that, you get

y = − 1 / 2 x + 3 / 2 y=-1/2x+3/2

y = − 3 / 4 + 7 / 4 y=-3/4+7/4

y = − 2 / 3 x + 4 / 3 y=-2/3x+4/3

y = − 4 / 5 x + 6 / 5 y=-4/5x+6/5

I did a little sketch of them and found that they do not form a quadrilateral nor do they meet at a single point; therefore, the answer is None of the given is true

PS: A picture to help visualize the problem .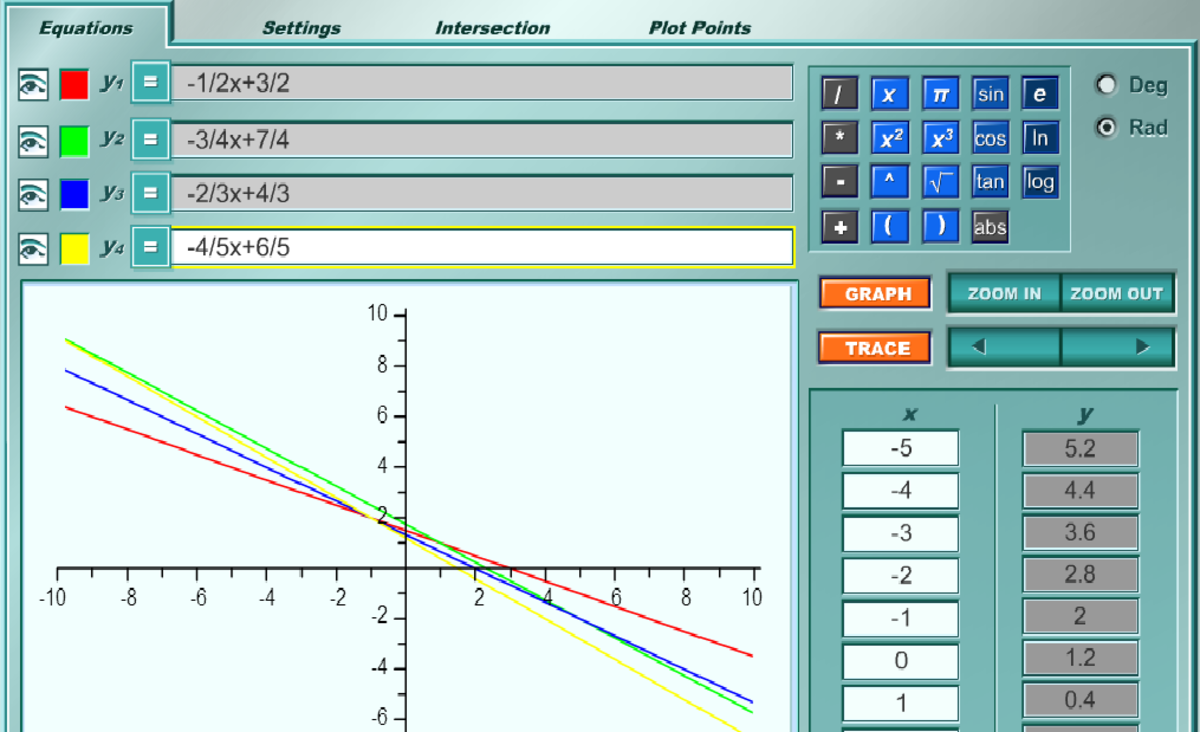

1 Helpful 0 Interesting 0 Brilliant 0 Confused

Umm, i found out a point of intersection, and saw all of them didnt satisfied which eliminates that concurrent one. Then I saw that if opposite angles had slope -ve of each other as tan(180-A)=-tan A. It also didnt happened. Then i checked for their points of intersection, they didnt even made a quadrilateral( I should have checked this first, then i shouldnt have to check for cyclic quad) and so the rem. one is None!

Md Zuhair - 3 years, 2 months ago

All have -tive slope between -1/2 and -4/5. There is no pattern either in slope or y-intercept. Sketching them shows first three line intersecting near (-1,2) and last one
passing them. Since three of them seem to intersect at a point, or very near one another, none of the other options is possible.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...