Question 13

Solution is really Long so here goes

1st Let us find the y-coordinates of the points of intersection of normal and tangent with Y-axis, Assuming a point P( $x_1,f(x_1))$

Point of intersection of Normal is : $y-f(x_1)=\frac{-1}{f'(x_1)}(0-x_1)$ , x-coordinate is 0

Point of intersection of tangent is : $y-f(x_1)=f'(x_1)(0-x_1)$ , x-coordinate is 0

As the midpoint of these 2 points is origin we add their y-coordinates and equate it to 0 to get a differential equation.

$0=2f(x)-x(f'(x)-\frac{1}{f'(x)})$ Also substituted $(x_1,y_1)$ as $(x,y)$

rearranging to get a quadratic, $(f'(x))^2-2\frac{y}{x}f'(x)-1=0$

taking its +ve root, writing $f'(x)$ as $\frac{dy}{dx}$ ...(It is given that slope is +ve in 1st quadrant)

$\frac{dy}{dx}=\frac{frac{2y}{x}+\sqrt{\frac{4y^2}{x^2}+1}}{2}$

\frac{dy}{dx}=\frac{y+\sqrt{y^2+x^2}{x}

Putting $y=tx$ to solve this differential equation,

we get equation as $t+\sqrt{1+t^2}=xc$ where c is constant of integration

resubstituting $t=frac{y}{x}$ and rearranging,

$y+\sqrt{x^2+y^2}=x^2c$

Using (3,4) we find c as 1. Now solve the 2 equations any way you want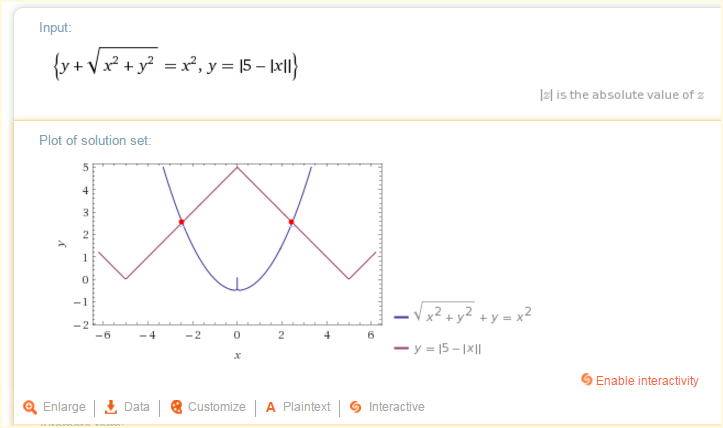

so answer is 2 solutions

I guesss the conic is a hyperbola....how to proceed further? my answer was a crude guess