Question -19
Calculus
Level
3
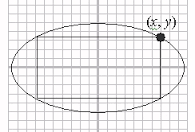Area of the greatest rectangle that can be inscribed in the ellipse
is :
Looking for Top Rank in JEE ? Alright, then go for this set : Expected JEE-Mains-2015-B .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
imagine a circlular ring placed in xy plane .and hence the z-coordinate value of every point of this ring i is zero now rotate it through some angle such that the axis of rotation is the x axis...if you imagine the way i am trying to explain....you will find some points of the ring get positive z cordinate value some get negative z cordinate vaue.....and their y cordionate value also decreases..........now try to see this ring from the same position you were seeing it as before.............you will see an ELLIPSE.THAT IS THE XY PROJECTION OF THIS RING WILL NOW LOOK AS ELLIPLSE.........................rectangle with max. area on the circle ring was a square whose vertices have x cordinate value +or - ( a/sqrt2).............the same square will now appear as a rectangle with maximum area...............the x cordinates would still be same.hence we would be able to trace the length and breadth of the rectangle.........and hence area
ellipse
THIS IS HOW I FEEL ELLIPSE..