Almost There

Let $a = 9999$

So , the given expression becomes -

$\sqrt{a^2 + 2a + 1}$

$=\sqrt{(a + 1)^2}$

$=a + 1$

$= 9999 + 1$

$=\boxed{10000}$

$\sqrt{9999 \times 9999+19999}$

= $\sqrt{9999 \times 9999+10000+9999}$

= $\sqrt{9999 \times (9999+1)+10000}$

= $\sqrt{9999 \times 10000+10000}$

= $\sqrt{10000 \times (9999+1)}$

=10000

$\begin{aligned} X & = \sqrt{9999\times 9999 + {\color{#3D99F6}19999}} \\ & = \sqrt{9999\times 9999 + {\color{#3D99F6}19998+1}} \\ & =\sqrt{{\color{#3D99F6}9999}^2 + 2({\color{#3D99F6}9999}) +1 } & \small {\color{#3D99F6} \text{Let } x = 9999} \\ & =\sqrt{{\color{#3D99F6}x}^2 + 2{\color{#3D99F6}x} +1} \\ & =\sqrt{(x+1)^2} \\ & = {\color{#3D99F6}x}+1 & \small {\color{#3D99F6} \text{Put back } x = 9999} \\ & = {\color{#3D99F6}9999}+1 \\ & = \boxed{10000} \end{aligned}$

9 x 9 = ends in 1, 1 + 9 ends in 0, 10000 is the only choice that ends in 0

$9999 = 10^4 - 1$

$19999 = 20000 - 1 = 2\times10^4 - 1$

$\sqrt{ (10^4 - 1)^2 + 2\times10^4 - 1}$

$\sqrt{ (10^4)^2 - 2\times10^4 + 1 + 2\times10^4 - 1}$

$\sqrt{ (10^4)^2} = 10^4 = 10000$

because 9x9 equals 81, and the ending number of the answet is 1. Also the ending number of 19999 is 9. 1+9 equals to 10, so only 10000 is thr answer.

A fast solution: Notice that 9999 × 9999 first digit is 1 and 19999 first digit is 9 so their sum must be a power of ten.. then 10000 must be the solution.

xyz9*xyz9=abcde1

abcde1+efgh9 = rtyub0

√rtyub0 should end with 0

The only answer that ends with 0 in choices is 10000

$\sqrt { { 9999 }\times 9999+19999 } \\ =\sqrt { { 9999 }^{ 2 }+19998+1 } \\ =\sqrt { { 9999 }^{ 2 }+2\times 9999\times 1+{ 1 }^{ 2 } } \\ =\sqrt { { (9999+1) }^{ 2 } } \\ =\sqrt { { 10000 }^{ 2 } } =\boxed{10000}$

We must find the square root of: $9999 * 9999 + 19999$ = $(10^4 - 1)^2 + 10^4 + 10^4 - 1$ = $(10^4 - 1)^2 + 2*10^4 - 1$ = A.

Let $x = 10^4$ . Then: A = $(x - 1)^2 + 2x - 1$ = $x^2 - 2x + 1 + 2x - 1$ = $x^2 = (10^4)^2$ . Then the root is clearly $10^4$ .

9x9 is 81. 81+9 = 90 which ends in a zero. The whole number of any square root of a number that ends in a zero must also end in a zero and there was only 1 answer that ended in a zero. Lateral thinking.

9x9 is 81.

81+9 = 90 which ends in a zero.

The whole number of any square root of a number that ends in a zero must also end in a zero and there was only 1 answer that ended in a zero

9*9=81 so the digit of the unity of the product is 1 and those of the other nomber is 9 do with the sum we will have a number like that under the square "xxxxxx0" because the last digit is a 0 the last digit of the result is a 0 too so only 10000 can be correct

9×9=81 take the "1" digit. 1+9=10 so it must be 10000, since the other answers end in other ways :')

Multiply 9 by 9, the result will give 1 (least significant bit). And when adding 9 receive 0 (least significant bit) and there is only one answer fits.

$\begin{aligned} \sqrt { 9999\times 9999+19999 } & = & \sqrt { { 9999 }^{ 2 }+9999+10000 } \\ \quad & = & \sqrt { { 9999 }^{ 2 }+9999+9999+1 } \\ \quad & = & \sqrt { { 9999 }^{ 2 }+2(9999)(1)+{ 1 }^{ 2 } } \\ \quad & = & \sqrt { { (9999+1) }^{ 2 } } \\ \quad & = & 9999+1 \\ \quad & = & \boxed { 10000 } \end{aligned}$

$\sqrt{9999 \times 9999+19999}=\sqrt{9999^2+10000+9999}=\sqrt{9999(9999+1)+10000}=\sqrt{9999(9999+1)+(9999+1)}=\sqrt{(9999+1)(9999+1)}=\sqrt{(9999+1)^2}=9999+1=\boxed{\large{10000}}$

LaTeX\(\sqrt{(10000-1)(10000-1)+ (2000 -1))} = $\sqrt{((10000^2 - 20000 + 1) + 2000 -1)}$ = $\sqrt{(10000^2)}$ (LaTeX(10000)

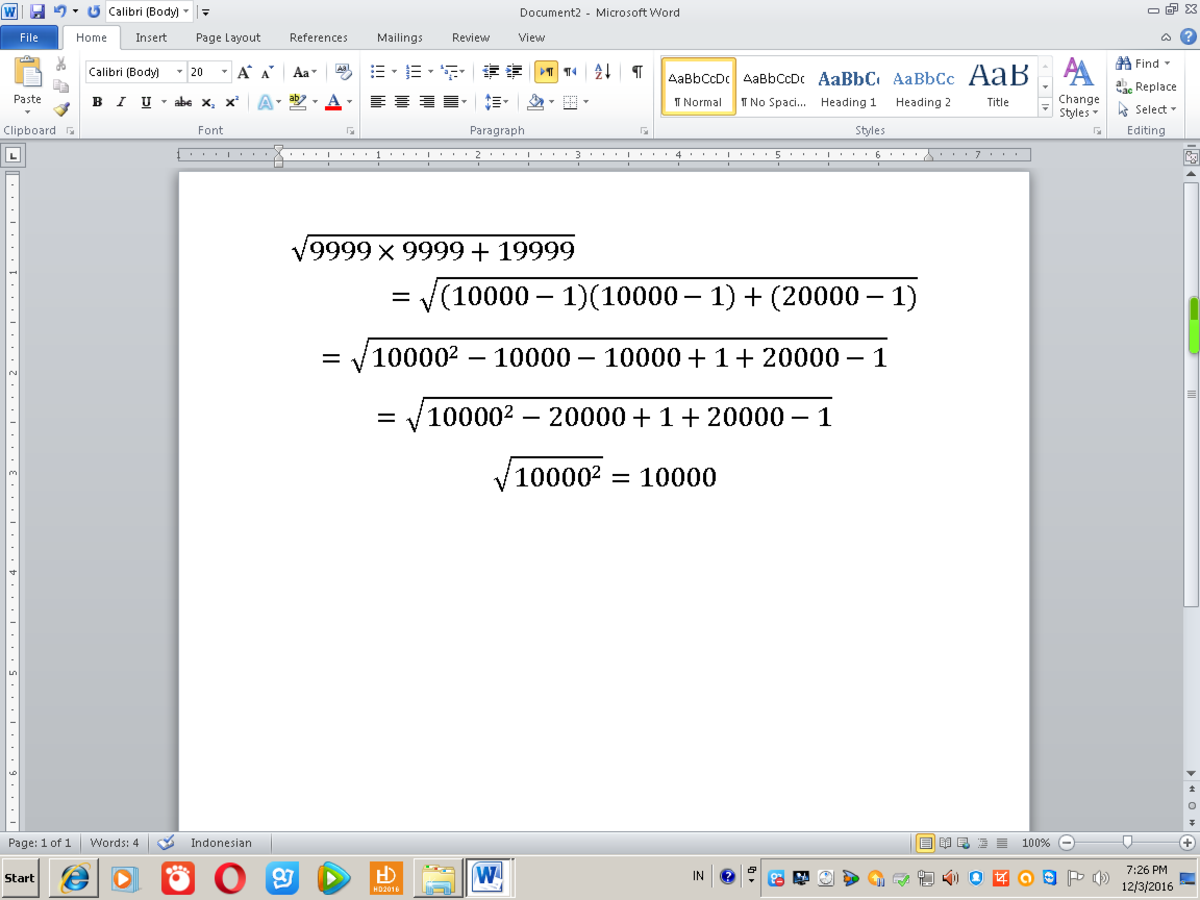
x =(10000-1)(10000-1) + 19999 =10000^2 +1 -2×10000 +19999 =10000^2 -20000 +20000 =10000^2 so x^1/2 = 10000

General solution: sqrt [ (10^n-1)^2 + 2 10^n - 1] = sqrt [ 10^(2n) + 1 - 2 10^n + 2*10^n - 1] = sqrt [ 10^(2n) ] = 10^n

For this problem, set n = 4 to get the correct answer, i.e. 10000.

you can figure any square, and it's square root, if you know what the previous square is. take the previous square, add its square root and the next highest number.

9999^2=99980001

10000^2=100000000

100000000-99980001=19999

19999-9999=10000

not sure anyone will follow that.

9x9 + 19 = 10 So let's bring back the other decimals. = 100000 Sqroute = 10000

Not the best way, but how I did it: You know that 9999 x 9999 ends with the digit 1 (because 9 x 9 = 81). Adding a number ending with the digit 1 will give a number that ends with the digit 0. The only choice that will have a square that ends with the digit 0 is 10000.

9999 X 9999 = 10000 ×9999 - 9999 So now √10000 ×9999 -9999 + 19999 =√ 10000×9999 +10000 = √10000( 9999 + 1 ) = √ 10000 ( 10000) = 10000

Why not (9999)(9999) then + 19999 = 100,000,000 and take the square of that?

Good quest

(99.99×100×99.99×100+1.9999×10000)^.5. =100×(99.99^2+1.9999)^.5=100×((100-.01)^2+1.9999)^.5=100×(10000+.0001-2+1.9999)^.5 =100×100=10000####

Let x= 10000

sqrt( (x-1)^2 +2x-1) sqrt(x^2-2x+1 +2x-1) sqrt(x^2) x

Therefore, the answer is 10000

9999 x 9999+ 9999 +10000 one extra lot of 9999 10000 x 9999 + 10000 Factorise 10000(9999 + 1) = 10000 x 10000 Therefore sqrt(10000 x 10000) = 10000