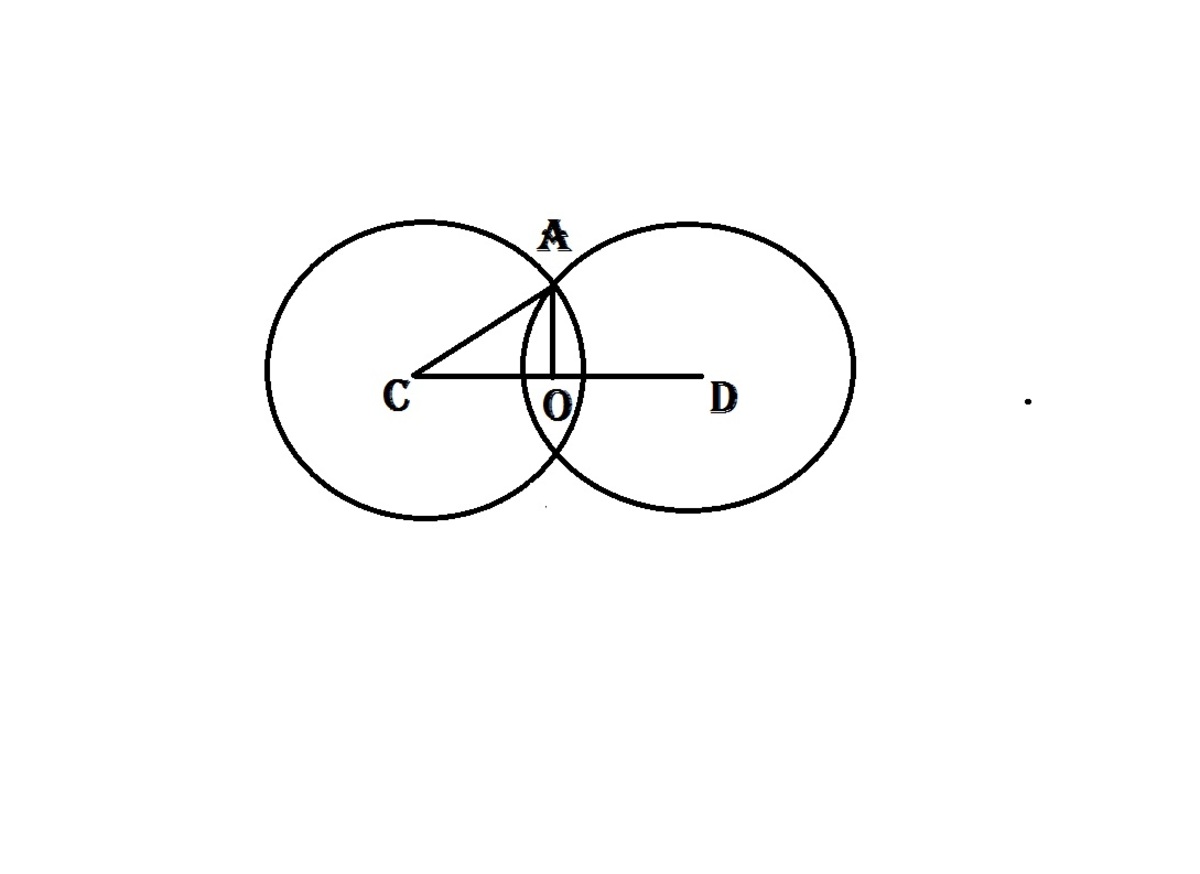Question -26

Geometry Level 3

The length of the common chord of two circles ( x − a ) 2 + ( y − b ) 2 = c 2 (x-a)^2+(y-b)^2=c^2 amd ( x − b ) 2 + ( y − a ) 2 = c 2 (x-b)^2+(y-a)^2=c^2 is:

Looking for Top Rank in JEE ? Alright, then go for this set : Expected JEE-Mains-2015-B .
4 c 2 + 2 ( a − b ) 2 \sqrt{4c^2+2(a-b)^2} 4 c 2 − 2 ( a − b ) 2 \sqrt{4c^2-2(a-b)^2} 4 c 2 − ( a − b ) 2 \sqrt{4c^2-(a-b)^2} 2 c 2 − 2 ( a − b ) 2 \sqrt{2c^2-2(a-b)^2}

View wiki
Sandeep Bhardwaj by Sandeep Bhardwaj , 28, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Nikhil Moghe
Mar 3, 2015

Distance B/w the Centers of the two circles Can be found by distance formula then half the distance b/w the centers in figure is OC .So by Pythagoras Theorem In Triangle AOC Find AO and then Double it ...... Here AC is the radius of the circles i.e. c

3 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...