Zero In On A Kaleidoscope

Geometry Level 1

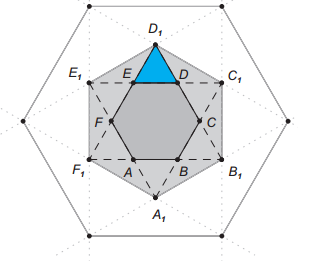
Extending the sides of a regular hexagon $ABCDEF$ , of an area of $1\text{ cm}^2$ , we get another hexagon $A_1B_1C_1D_1E_1F_1$ .

Repeating this process, we can get other hexagons $A_2B_2C_2D_2E_2F_2$ etc.

What is the area of the blue triangle?

\frac{1}{3}

\frac{1}{6}

\frac{1}{8}

\frac{1}{9}

2 solutions

Sundeep Kalyan
Apr 10, 2016

As regular hexagon can be divided into six equilateral triangles therefore, each triangle has area1/6square cm and blue triangle is congruent to each equilateral triangle so area of blue triangle is1/6

Caique Harger
Apr 10, 2016

You can divide the hexagon in 6 equilaterals triangles, as the blue triangle is formed by the extension of the sides it have the same angles só it is also equilateral with the same size of the triangles you created inside the hexagon. So the area of onde inside triangle is the same of the blue one that is 1/6 ( as the hexagon area is 1 and you have 6 triangles)

Zero In On A Kaleidoscope

2 solutions

0 pending reports